What is an Outlier?

In statistics, an outlier is an observation that is numerically distant from the rest of the data. Outliers can occur by chance in any distribution, but they are often indicative either of measurement error or of the population having a heavy-tailed distribution. In the former case, one wishes to discard the outliers or use statistics that are robust against them. In the latter case, outliers indicate that the distribution is skewed and that one should be very cautious in using tools or intuitions that assume a normal distribution.

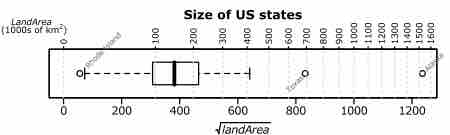
Outliers

This box plot shows where the US states fall in terms of their size. Rhode Island, Texas, and Alaska are outside the normal data range, and therefore are considered outliers in this case.

In most larger samplings of data, some data points will be further away from the sample mean than what is deemed reasonable. This can be due to incidental systematic error or flaws in the theory that generated an assumed family of probability distributions, or it may be that some observations are far from the center of the data. Outlier points can therefore indicate faulty data, erroneous procedures, or areas where a certain theory might not be valid. However, in large samples, a small number of outliers is to be expected, and they typically are not due to any anomalous condition.

Outliers, being the most extreme observations, may include the sample maximum or sample minimum, or both, depending on whether they are extremely high or low. However, the sample maximum and minimum are not always outliers because they may not be unusually far from other observations.

Interpretations of statistics derived from data sets that include outliers may be misleading. For example, imagine that we calculate the average temperature of 10 objects in a room. Nine of them are between 20° and 25° Celsius, but an oven is at 175°C. In this case, the median of the data will be between 20° and 25°C, but the mean temperature will be between 35.5° and 40 °C. The median better reflects the temperature of a randomly sampled object than the mean; however, interpreting the mean as "a typical sample", equivalent to the median, is incorrect. This case illustrates that outliers may be indicative of data points that belong to a different population than the rest of the sample set. Estimators capable of coping with outliers are said to be robust. The median is a robust statistic, while the mean is not.

Causes for Outliers

Outliers can have many anomalous causes. For example, a physical apparatus for taking measurements may have suffered a transient malfunction, or there may have been an error in data transmission or transcription. Outliers can also arise due to changes in system behavior, fraudulent behavior, human error, instrument error or simply through natural deviations in populations. A sample may have been contaminated with elements from outside the population being examined. Alternatively, an outlier could be the result of a flaw in the assumed theory, calling for further investigation by the researcher.

Unless it can be ascertained that the deviation is not significant, it is ill-advised to ignore the presence of outliers. Outliers that cannot be readily explained demand special attention.

Identifying Outliers

There is no rigid mathematical definition of what constitutes an outlier. Thus, determining whether or not an observation is an outlier is ultimately a subjective exercise. Model-based methods, which are commonly used for identification, assume that the data is from a normal distribution and identify observations which are deemed "unlikely" based on mean and standard deviation. Other methods flag observations based on measures such as the interquartile range (IQR). For example, some people use the $1.5 \cdot \text{IQR}$ rule. This defines an outlier to be any observation that falls $1.5 \cdot \text{IQR}$ below the first quartile or any observation that falls $1.5 \cdot \text{IQR}$ above the third quartile.

Working With Outliers

Deletion of outlier data is a controversial practice frowned on by many scientists and science instructors. While mathematical criteria provide an objective and quantitative method for data rejection, they do not make the practice more scientifically or methodologically sound -- especially in small sets or where a normal distribution cannot be assumed. Rejection of outliers is more acceptable in areas of practice where the underlying model of the process being measured and the usual distribution of measurement error are confidently known. An outlier resulting from an instrument reading error may be excluded, but it is desirable that the reading is at least verified.

Even when a normal distribution model is appropriate to the data being analyzed, outliers are expected for large sample sizes and should not automatically be discarded if that is the case. The application should use a classification algorithm that is robust to outliers to model data with naturally occurring outlier points. Additionally, the possibility should be considered that the underlying distribution of the data is not approximately normal, but rather skewed.