In inferential statistics, data from a sample is used to "estimate" or "guess" information about the data from a population. Point estimation involves the use of sample data to calculate a single value or point (known as a statistic) which serves as the "best estimate" of an unknown population parameter. The point estimate of the mean is a single value estimate for a population parameter. The most unbiased point estimate of a population mean (µ) is the sample mean (
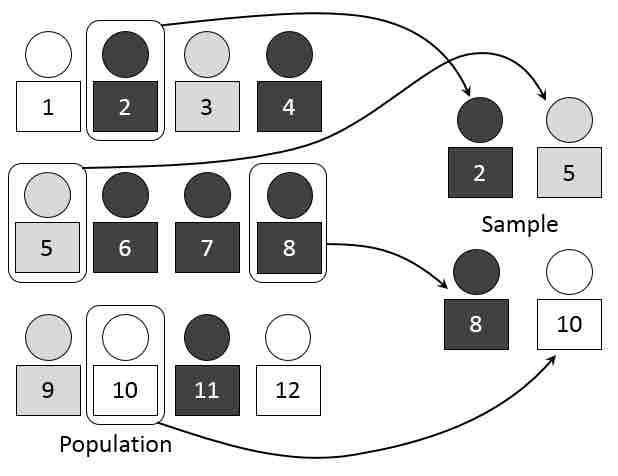
Simple random sampling of a population
We use point estimators, such as the sample mean, to estimate or guess information about the data from a population. This image visually represents the process of selecting random number-assigned members of a larger group of people to represent that larger group.
Maximum Likelihood
A popular method of estimating the parameters of a statistical model is maximum-likelihood estimation (MLE). When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters. The method of maximum likelihood corresponds to many well-known estimation methods in statistics. For example, one may be interested in the heights of adult female penguins, but be unable to measure the height of every single penguin in a population due to cost or time constraints. Assuming that the heights are normally (Gaussian) distributed with some unknown mean and variance, the mean and variance can be estimated with MLE while only knowing the heights of some sample of the overall population. MLE would accomplish this by taking the mean and variance as parameters and finding particular parametric values that make the observed results the most probable, given the model.
In general, for a fixed set of data and underlying statistical model, the method of maximum likelihood selects the set of values of the model parameters that maximizes the likelihood function. Maximum-likelihood estimation gives a unified approach to estimation, which is well-defined in the case of the normal distribution and many other problems. However, in some complicated problems, maximum-likelihood estimators are unsuitable or do not exist.
Linear Least Squares
Another popular estimation approach is the linear least squares method. Linear least squares is an approach fitting a statistical model to data in cases where the desired value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model (as in regression). The resulting fitted model can be used to summarize the data, to estimate unobserved values from the same system, and to understand the mechanisms that may underlie the system.
Mathematically, linear least squares is the problem of approximately solving an over-determined system of linear equations, where the best approximation is defined as that which minimizes the sum of squared differences between the data values and their corresponding modeled values. The approach is called "linear" least squares since the assumed function is linear in the parameters to be estimated. In statistics, linear least squares problems correspond to a statistical model called linear regression which arises as a particular form of regression analysis. One basic form of such a model is an ordinary least squares model.