The margin of error is a statistic used to analyze data. It expresses the amount of random sampling error in a survey's results. The larger the margin of error, the less faith one should have that the poll's reported results are close to the "true" figures—the figures for the whole population .
Margin of Error
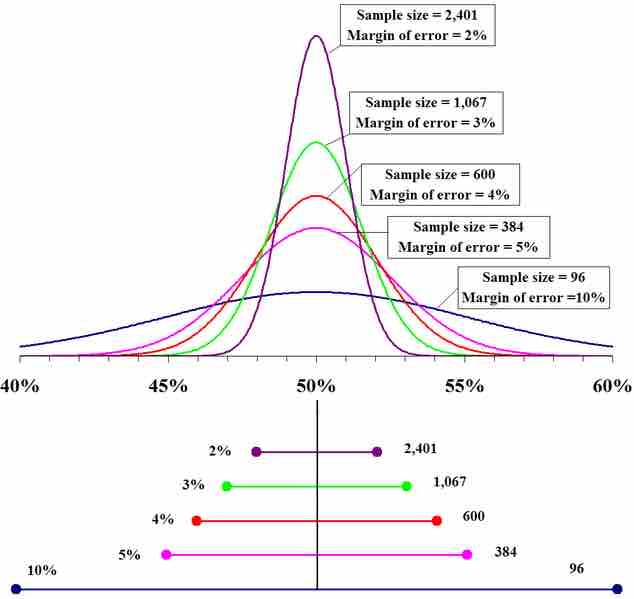
This normal distribution curve illustrates the points of various margin of errors.
Explanation
The margin of error is usually defined as the "radius" of a confidence interval for a particular statistic from a survey. When a single, global margin of error is reported for a survey, it refers to the maximum margin of error for all reported percentages using the full sample from the survey. If the statistic is a percentage, this maximum margin of error can be calculated as the radius of the confidence interval for a reported percentage of 50%.
The margin of error can be described as an "absolute" quantity. For example, if the true value is 50 percentage points, and the statistic has a confidence interval radius of 5 percentage points, then we say the margin of error is 5 percentage points.
However, the margin of error can also be expressed as a "relative" quantity. For example, suppose the true value is 50 people and the statistic has a confidence interval radius of 5 people. If we use the "relative" definition, then we express this absolute margin of error as a percent of the true value. Therefore, the absolute margin of error is 5 people, but the "percent relative" margin of error is 10% (because 5 people are ten percent of 50 people).
The margin of error can be defined for any desired confidence level, but usually a level of 90%, 95%, or 99% is chosen. This level is the probability that a margin of error around the reported percentage would include the "true" percentage. The confidence level, the sample design for a survey, and in particular its sample size, determines the magnitude of the margin of error. A larger sample size produces a smaller margin of error, all else remaining equal.
If the exact confidence intervals are used the margin of error takes into account both sampling error and non-sampling error. If an approximate confidence interval is used then the margin of error may only take random sampling error into account. It does not represent other potential sources of error or bias such as a non-representative sample-design, poorly phrased questions, people lying or refusing to respond, the exclusion of people who could not be contacted, or miscounts and miscalculations.
Basic Concept
Polls typically involve taking a sample from a certain population. In the case of the Newsweek 2004 Presidential Election poll, the population of interest was the population of people who would vote. Sampling theory provides methods for calculating the probability that the poll results differ from reality by more than a certain amount simply due to chance. For example, if the poll reports 47% for Kerry, his support could actually be as high as 50% or as low as 44%. The more people that are sampled, the more confident pollsters can be that the "true" percentage is close to the observed percentage. The margin of error is a measure of how close the results are likely to be.
Effect of Population Size
The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is less than 5%.
In cases where the sampling fraction exceeds 5%, analysts can adjust the margin of error using a "finite population correction" (FPC) to account for the added precision gained by sampling a larger percentage of the population.
The FPC, factored into the calculation of the margin of error, has the effect of narrowing the margin of error. It holds that the FPC approaches zero as the sample size approaches the population size, which has the effect of eliminating the margin of error entirely.
Comparing Percentages
The terms "statistical tie" and "statistical dead heat" are sometimes used to describe reported percentages that differ by less than a margin of error, but these terms can be misleading. For one thing, the margin of error as generally calculated is applicable to an individual percentage and not the difference between percentages. The difference between two percentage estimates may not be statistically significant even when they differ by more than the reported margin of error. The survey results also usually provide strong information even when there is not a statistically significant difference.