Understanding the Restoring Force
Newton's first law implies that an object oscillating back and forth is experiencing forces. Without force, the object would move in a straight line at a constant speed rather than oscillate. It is important to understand how the force on the object depends on the object's position. If an object is vibrating to the right and left, then it must have a leftward force on it when it is on the right side, and a rightward force when it is on the left side. In one dimension, we can represent the direction of the force using a positive or negative sign, and since the force changes from positive to negative there must be a point in the middle where the force is zero. This is the equilibrium point, where the object would stay at rest if it was released at rest. It is common convention to define the origin of our coordinate system so that x equals zero at equilibrium .
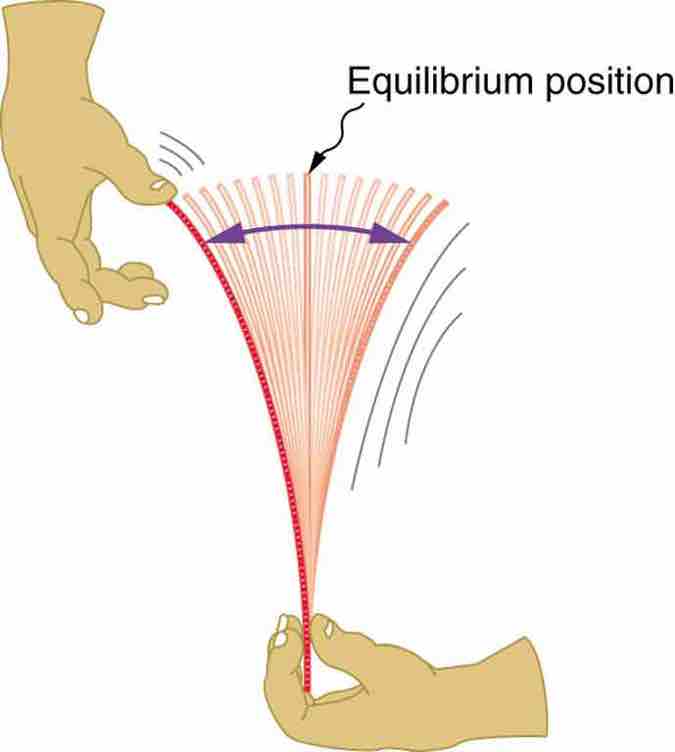
Oscillating Ruler
When displaced from its vertical equilibrium position, this plastic ruler oscillates back and forth because of the restoring force opposing displacement. When the ruler is on the left, there is a force to the right, and vice versa.
Consider, for example, plucking a plastic ruler shown in the first figure. The deformation of the ruler creates a force in the opposite direction, known as a restoring force. Once released, the restoring force causes the ruler to move back toward its stable equilibrium position, where the net force on it is zero. However, by the time the ruler gets there, it gains momentum and continues to move to the right, producing the opposite deformation. It is then forced to the left, back through equilibrium, and the process is repeated until dissipative forces (e.g., friction) dampen the motion. These forces remove mechanical energy from the system, gradually reducing the motion until the ruler comes to rest .
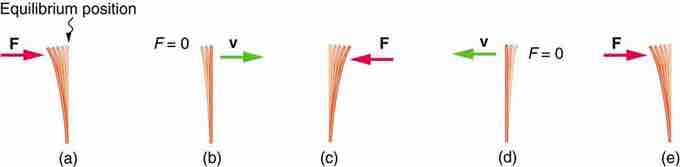
Restoring force, momentum, and equilibrium
(a) The plastic ruler has been released, and the restoring force is returning the ruler to its equilibrium position. (b) The net force is zero at the equilibrium position, but the ruler has momentum and continues to move to the right. (c) The restoring force is in the opposite direction. It stops the ruler and moves it back toward equilibrium again. (d) Now the ruler has momentum to the left. (e) In the absence of damping (caused by frictional forces), the ruler reaches its original position. From there, the motion will repeat itself.
Hooke's Law
The simplest oscillations occur when the restoring force is directly proportional to displacement. The name that was given to this relationship between force and displacement is Hooke's law:
Here, F is the restoring force, x is the displacement from equilibrium or deformation, and k is a constant related to the difficulty in deforming the system (often called the spring constant or force constant). Remember that the minus sign indicates the restoring force is in the direction opposite to the displacement. The force constant k is related to the rigidity (or stiffness) of a system—the larger the force constant, the greater the restoring force, and the stiffer the system. The units of k are newtons per meter (N/m). For example, k is directly related to Young's modulus when we stretch a string. A typical physics laboratory exercise is to measure restoring forces created by springs, determine if they follow Hooke's law, and calculate their force constants if they do .
Mass on a Spring
A common example of an objecting oscillating back and forth according to a restoring force directly proportional to the displacement from equilibrium (i.e., following Hooke's Law) is the case of a mass on the end of an ideal spring, where "ideal" means that no messy real-world variables interfere with the imagined outcome.
The motion of a mass on a spring can be described as Simple Harmonic Motion (SHM), the name given to oscillatory motion for a system where the net force can be described by Hooke's law. We can now determine how to calculate the period and frequency of an oscillating mass on the end of an ideal spring. The period T can be calculated knowing only the mass, m, and the force constant, k:
When dealing with
We can understand the dependence of these equations on m and k intuitively. If one were to increase the mass on an oscillating spring system with a given k, the increased mass will provide more inertia, causing the acceleration due to the restoring force F to decrease (recall Newton's Second Law:

Motion of a mass on an ideal spring
An object attached to a spring sliding on a frictionless surface is an uncomplicated simple harmonic oscillator. When displaced from equilibrium, the object performs simple harmonic motion that has an amplitude X and a period T. The object's maximum speed occurs as it passes through equilibrium. The stiffer the spring is, the smaller the period T. The greater the mass of the object is, the greater the period T. (a) The mass has achieved its greatest displacement X to the right and now the restoring force to the left is at its maximum magnitude. (b) The restoring force has moved the mass back to its equilibrium point and is now equal to zero, but the leftward velocity is at its maximum. (c) The mass's momentum has carried it to its maximum displacement to the right. The restoring force is now to the right, equal in magnitude and opposite in direction compared to (a). (d) The equilibrium point is reach again, this time with momentum to the right. (e) The cycle repeats.