Entropy is a measure of disorder. This notion was initially postulated by Ludwig Boltzmann in the 1800s. For example, melting a block of ice means taking a highly structured and orderly system of water molecules and converting it into a disorderly liquid in which molecules have no fixed positions . There is a large increase in entropy in the process.
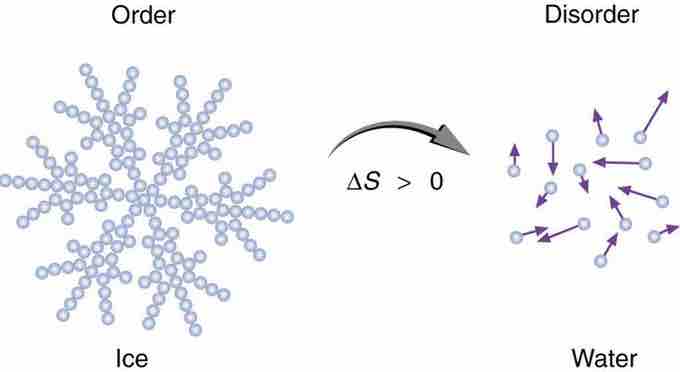
Entropy of Ice
When ice melts, it becomes more disordered and less structured. The systematic arrangement of molecules in a crystal structure is replaced by a more random and less orderly movement of molecules without fixed locations or orientations. Its entropy increases because heat transfer occurs into it. Entropy is a measure of disorder.
Example
As an example, suppose we mix equal masses of water originally at two different temperatures, say 20.0º C and 40.0º C. The result is water at an intermediate temperature of 30.0º C. Three outcomes have resulted:
- Entropy has increased.
- Some energy has become unavailable to do work.
- The system has become less orderly.
Entropy, Energy, and Disorder
Let us think about each of the results. First, entropy has increased for the same reason that it did in the example above. Mixing the two bodies of water has the same effect as heat transfer from the hot one and the same heat transfer into the cold one. The mixing decreases the entropy of the hot water but increases the entropy of the cold water by a greater amount, producing an overall increase in entropy.
Second, once the two masses of water are mixed, there is only one temperature—you cannot run a heat engine with them. The energy that could have been used to run a heat engine is now unavailable to do work.
Third, the mixture is less orderly, or to use another term, less structured. Rather than having two masses at different temperatures and with different distributions of molecular speeds, we now have a single mass with a uniform temperature.
These three results—entropy, unavailability of energy, and disorder—are not only related but are in fact essentially equivalent.