An isothermal process is a change of a system in which the temperature remains constant: ΔT = 0. Typically this occurs when a system is in contact with an outside thermal reservoir (heat bath), and the change occurs slowly enough to allow the system to adjust continually to the temperature of the reservoir through heat exchange. In contrast, an adiabatic process occurs when a system exchanges no heat with its surroundings (Q = 0). In other words, in an isothermal process, the value ΔT = 0 but Q ≠ 0, while in an adiabatic process, ΔT ≠ 0 but Q = 0.
For an ideal gas, the product PV (P: pressure, V: volume) is a constant if the gas is kept at isothermal conditions (Boyle's law). According to the ideal gas law, the value of the constant is NkT, where N is the number of molecules of gas and k is Boltzmann's constant.
This means that
The family of curves generated by this equation is shown in the graph presented in . Each curve is called an isotherm. Such graphs are termed indicator diagrams—first used by James Watt and others to monitor the efficiency of engines. The temperature corresponding to each curve in the figure increases from the lower left to the upper right.
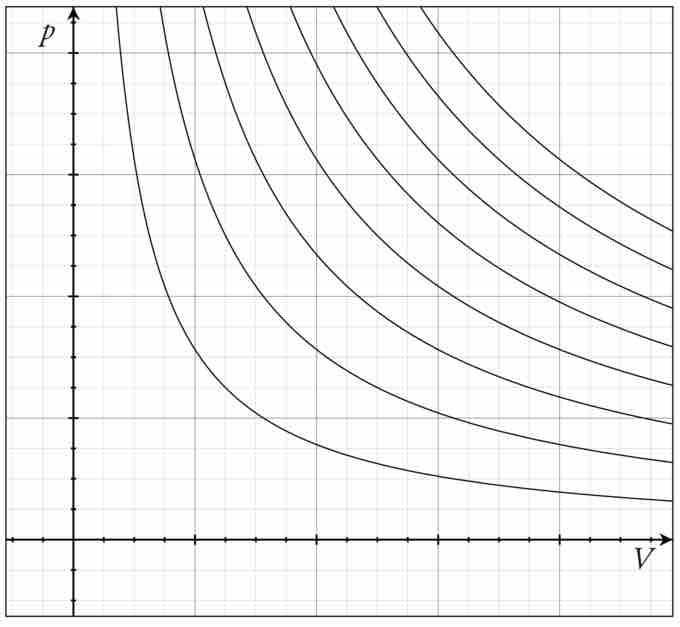
Isotherms of an Ideal Gas
Several isotherms of an ideal gas on a PV diagram.
Calculation of Work
In thermodynamics, the work involved when a gas changes from state A to state B is simply:
(This equation is derived in our Atom on "Constant Pressure" under kinetic theory. Note that P = F/A. This definition is consistent with our definition of work being force times distance. )
For an isothermal, reversible process, this integral equals the area under the relevant pressure-volume isotherm, and is indicated in blue in for an ideal gas. Again, P = nRT / V applies and with T being constant (as this is an isothermal process), we have:
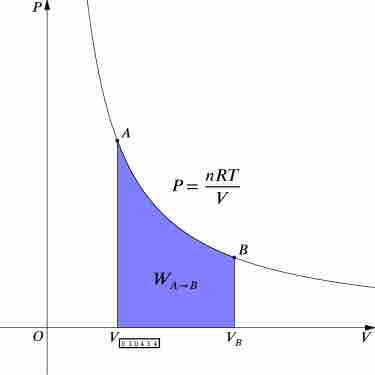
Work Done by Gas During Expansion
The blue area represents "work" done by the gas during expansion for this isothermal change.
By convention, work is defined as the work the system does on its environment. If, for example, the system expands by a piston moving in the direction of force applied by the internal pressure of a gas, then the work is counted as positive. As this work is done by using internal energy of the system, the result is that the internal energy decreases. Conversely, if the environment does work on the system so that its internal energy increases, the work is counted as negative (for details on internal energy, check our Atom on "Internal Energy of an Ideal Gas").