A standing wave is a wave that appears stationary, meaning it remains in a constant position. In a string, a standing wave is a type of transverse wave—where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. A standing wave can occur when two identical waves moving in different directions along the string interfere.
There are two scenarios of waves in strings: the string is fixed at both ends, or the string is fixed at one end and free at the other. A transverse wave will move along the string until it reaches the other end. It is then reflected from that end and starts to move back towards the original direction; at this point interference occurs. shows a transverse wave that is reflected from a fixed end. When a transverse wave meets a fixed end, the wave is reflected, but inverted. This swaps the peaks with the troughs and the troughs with the peaks. diagrams a transverse wave on a string that meets a free end. The wave is reflected, but unlike a transverse wave with a fixed end, it is not inverted.

Free End Reflection
The wave is reflected, but unlike a transverse wave with a fixed end, it is not inverted.

Fixed End Reflection
When a transverse wave meets a fixed end, the wave is reflected, but inverted.
Standing Waves
When either of the two scenarios of wave reflection occurs, the incident wave meets the reflected wave. These waves move past each other in opposite directions, causing interference. When these two waves have the same frequency, the product of this is called the standing waves. Standing waves appear to be standing still, hence the name. illustrates a very slow moving standing wave. (One application of the principle of standing waves is in music with the concept of resonance—and how many musical instruments, like guitars and pianos, get their sound. ) Let us now examine how standing waves occur.
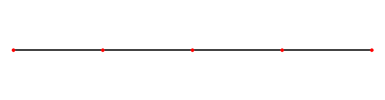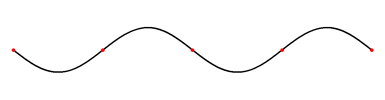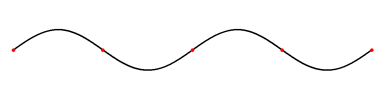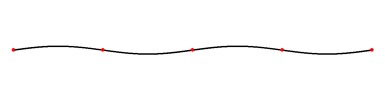
Standing Wave on a String
This is what a standing wave would look like if you were to slow it down. The wave is caused by an incident wave on a string being reflected and then traveling back in the direction it came from. The two waves then meet and interfere with each other causing this phenomenon.
Constructive vs. Destructive Interference
When the incident wave and reflected wave first meet, both waves have an amplitude is zero. As the waves continue to move past each other they continue to interfere with each other, either constructively of destructively. As discussed in previous atoms, when waves are completely in phase and interfere with each other constructively they are amplified, and when they are completely out of phase and interfere destructively they cancel out. As the waves continue to move past each other, and are reflected from the opposite end, they continue to interfere both ways; a standing wave is produced. Every point in the medium containing a standing wave oscillates up and down, and the amplitude of the oscillations depends on the location of the point. When we observe a standing wave on strings, it appears the wave is not moving but standing still. In summary:
- The points which reach the maximum oscillation height are called antinodes, and are results of complete constructive interference.
- The points in a standing wave that appear to remain flat and do not move are called nodes. These are due to complete destructive interference.