Solving Problems with Vectors and Coulomb's Law
Electric Force Between Two Point Charges
To address the electrostatic forces among electrically charged particles, first consider two particles with electric charges q and Q , separated in empty space by a distance r. Suppose that we want to find the electric force vector on charge q. (The electric force vector has both a magnitude and a direction. ) We can express the location of charge q as rq, and the location of charge Q as rQ. In this way we can know both how strong the electric force is on a charge, but also what direction that force is directed in. Coulomb's Law using vectors can be written as:
In this equation, k is equal to
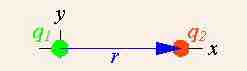
This vector notation can be used in the simple example of two point charges where only one of which is a source of charge .
Application of Coulomb's Law
In a simple example, the vector notation of Coulomb's Law can be used when there are two point charges and only one of which is a source charge.
Electric Force on a Field Charge Due to Fixed Source Charges
Suppose there is more than one point source charges providing forces on a field charge. diagrams a fairly simple example with three source charges (shown in green and indexed by subscripts) and one field charge (in red, designated q). We assume that the source charges are fixed in space, and the field charge q is subject to forces from the source charges.
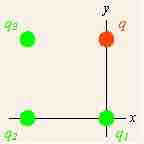
Multiple point charges
Coulomb's Law applied to more than one point source charges providing forces on a field charge.
Note the coordinate system that has been chosen. All of the charges lie on the corners of a square, and the origin is chosen to collocate with the lower right source charge, and aligned with the square. Since we can have only one origin of coordinates, no more than one of the source points can lie at the origin, and the displacements from different source points to the field point differ. The total force on the field charge q is due to applications of the force described in the vector notation of Coulomb's Law from each of the source charges. The total force is therefore the sum of these individual forces .
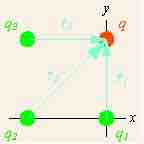
Displacements of field charge
The displacements of the field charge from each source charge are shown as light blue arrows.
Applying Coulomb's Law three times and summing the results gives us:
This equation can further be simplified and applied to a fixed number of charge points.