Profit Maximization Function for Monopolies

Monopolies have much more power than firms normally would in competitive markets, but they still face limits determined by demand for a product. Higher prices (except under the most extreme conditions) mean lower sales. Therefore, monopolies must make a decision about where to set their price and the quantity of their supply to maximize profits. They can either choose their price, or they can choose the quantity that they will produce and allow market demand to set the price.

Since costs are a function of quantity, the formula for profit maximization is written in terms of quantity rather than in price. The monopoly's profits are given by the following equation:

π=p(q)q−c(q)

In this formula, p(q) is the price level at quantity q. The cost to the firm at quantity q is equal to c(q). Profits are represented by π. Since revenue is represented by pq and cost is c, profit is the difference between these two numbers. As a result, the first-order condition for maximizing profits at quantity q is represented by:

0=∂q=p(q)+qp′(q)−c′(q)

The above first-order condition must always be true if the firm is maximizing its profit - that is, if p(q)+qp′(q)−c′(q) is not equal to zero, then the firm can change its price or quantity and make more profit. 

Marginal revenue is calculated by p(q)+qp′(q), which is derived from the term for revenue, pq. The term c′(q) is marginal cost, which is the derivative of c(q). Monopolies will produce at quantity q where marginal revenue equals marginal cost. Then they will charge the maximum price p(q) that market demand will respond to at that quantity.

Consider the example of a monopoly firm that can produce widgets at a cost given by the following function:

c(q)=2+3q+q²

If the firm produces two widgets, for example, the total cost is 2+3(2)+2²=12. The price of widgets is determined by demand:

p(q)=24-2p

When the firm produces two widgets it can charge a price of 24-2(2)=20 for each widget. The firm's profit, as shown above, is equal to the difference between the quantity produces multiplied by the price, and the total cost of production: p(q)q−c(q). How can we maximize this function?

Using the first order condition, we know that when profit is maximized, 0=p(q)+qp′(q)−c′(q). In this case:

0=(24-2p)+q(-2)-(3+2q)=21-6q

Rearranging the equation shows that q=3.5. This is the profit maximizing quantity of production.

Consider the diagram illustrating monopoly competition . The key points of this diagram are fivefold.

1. First, marginal revenue lies below the demand curve. This occurs because marginal revenue is the demand, p(q), plus a negative number.
2. Second, the monopoly quantity equates marginal revenue and marginal cost, but the monopoly price is higher than the marginal cost.
3. Third, there is a deadweight loss, for the same reason that taxes create a deadweight loss: The higher price of the monopoly prevents some units from being traded that are valued more highly than they cost.
4. Fourth, the monopoly profits from the increase in price, and the monopoly profit is illustrated.
5. Fifth, since—under competitive conditions—supply equals marginal cost, the intersection of marginal cost and demand corresponds to the competitive outcome.

We see that the monopoly restricts output and charges a higher price than would prevail under competition.

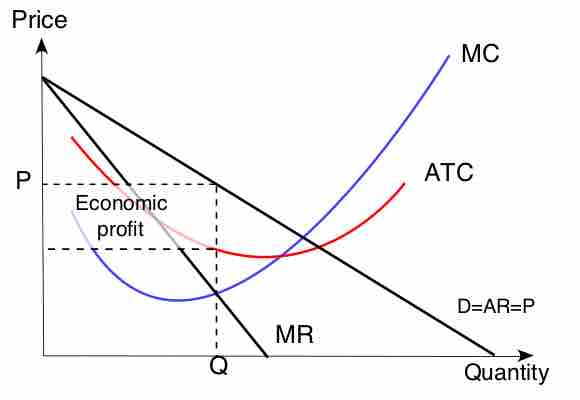
Monopoly Diagram

This graph illustrates the price and quantity of the market equilibrium under a monopoly.