A surface is a two-dimensional, topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space
To say that a surface is "two-dimensional" means that, about each point, there is a coordinate patch on which a two-dimensional coordinate system is defined. For example, the surface of the Earth is (ideally) a two-dimensional surface, and latitude and longitude provide two-dimensional coordinates on it (except at the poles and along the 180th meridian).
The concept of surface finds application in physics, engineering, computer graphics, and many other disciplines, primarily in representing the surfaces of physical objects. For example, in analyzing the aerodynamic properties of an airplane, the central consideration is the flow of air along its surface.
Historically, surfaces were initially defined as subspaces of Euclidean spaces. Often, these surfaces were the locus of zeros of certain functions, usually polynomial functions. Such a definition considered the surface as part of a larger (Euclidean) space, and as such was termed extrinsic.
Example
In Cartesian coordinates, a sphere can be defined parametrically—e.g., by:
or implicitly—e.g., by:
In spherical coordinates, the surface can be expressed simply by
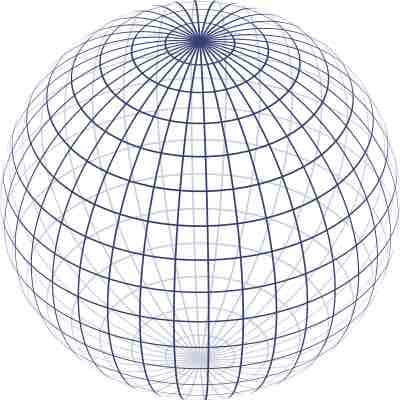
A Sphere Defined Parametrically
A sphere can be defined parametrically or implicitly.