Vector-Valued Functions

What is a Vector Valued Function?

Also called vector functions, vector valued functions allow you to express the position of a point in multiple dimensions within a single function. These can be expressed in an infinite number of dimensions, but are most often expressed in two or three. The input into a vector valued function can be a vector or a scalar. In this atom we are going to introduce the properties and uses of the vector valued functions.

Properties of Vector Valued Functions

A vector valued function allows you to represent the position of a particle in one or more dimensions. A three-dimensional vector valued function requires three functions, one for each dimension. In Cartesian form with standard unit vectors (i,j,k), a vector valued function can be represented in either of the following ways:

$\mathbf{r}(t) = f(t)\mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}\\ \mathbf{r}(t) = \langle f(t) , g(t) , h(t) \rangle$

where $t$ is being used as the variable. This is a three dimensional vector valued function. The graph shows a visual representation of

$\mathbf{r}(t) = \langle 2 \cos(t) , 4 \sin(t) , t \rangle$.

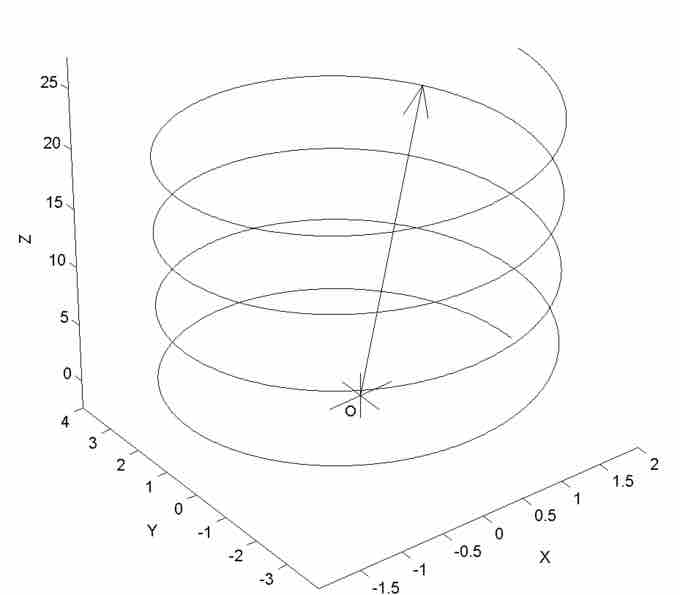
Vector-Valued Function

This a graph of a parametric curve (a simple vector-valued function with a single parameter of dimension $1$). The graph is of the curve: $\langle 2 \cos(t), 4 \sin(t),t \rangle$ where $t$ goes from $0$ to $8 \pi$.

This can be broken down into three separate functions called component functions:

$x(t) = 2 \cos(t)y(t) = 4 \sin(t)z(t) = t$.

If you were to take a cross section, with the cut perpendicular to any of the three axes, you would see the graph of that function. For example, if you were to slice the three-dimensional shape perpendicular to the $z$-axis, the graph you would see would be of the function $z(t)=t$.The domain of a vector valued function is a domain that satisfies all of the component functions. It can be found by taking the intersection of the individual component function domains. The vector valued functions can be manipulated in the same way as a vector; they can be added, subtracted, and the dot product and the cross product can be found.

Example

For this example, we will use time as our parameter. The following vector valued function represents time, $t$: 

$\mathbf{r}(t) = f(t)\mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}$

This function is representing a position. Therefore, if we take the derivative of this function, we will get the velocity:

$\displaystyle{\frac{d\mathbf{r}(t)}{dt}= f(t)\mathbf{i}' + g(t)\mathbf{j}' + h(t)\mathbf{k}' \\ \,\qquad = \mathbf{v}(t)\\ }$ 

If we differentiate a second time, we will be left with acceleration:

$\displaystyle{\frac{d\mathbf{v}(t)}{dt}= \mathbf{a}(t)}$