Calculus of Vector-Valued Functions

A vector-valued function, also referred to as a vector function, is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector. The dimension of the domain is not defined by the dimension of the range.

A common example of a vector valued function is one that depends on a single real number parameter $t$, often representing time, producing a vector $\mathbf{v}(t)$ as the result. In terms of the standard unit vectors $\mathbf{i}$, $\mathbf{j}$, $\mathbf{k}$ of Cartesian 3-space, these specific type of vector-valued functions are given by expressions such as:

$\mathbf{r}(t) = f(t)\mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}$

where $f(t)$, $g(t)$, and $h(t)$ are the coordinate functions of the parameter $t$. The vector $\mathbf{v}(t)$ has its tail at the origin and its head at the coordinates evaluated by the function.

Vector functions can also be referred to in a different notation:

$\mathbf{r}(t)=\langle f(t), g(t), h(t)\rangle$

Vector valued function

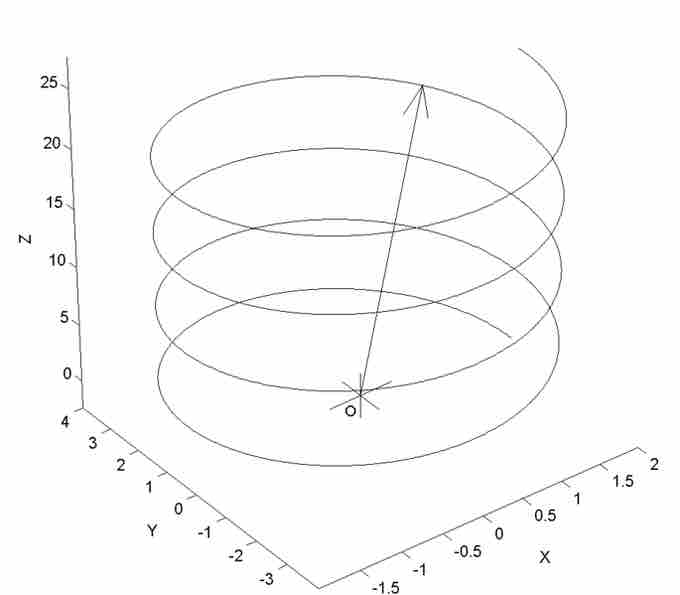
This graph is a visual representation of the three-dimensional vector-valued function $\mathbf{r}(t) = \langle 2 \cos(t) , 4 \sin(t) , t \rangle$. This can be broken down into three separate functions called component functions: $x(t) = 2 \cos(t)y(t) = 4 \sin(t)z(t) = t$.

Vector calculus is a branch of mathematics that covers differentiation and integration of vector fields in any number of dimensions. Because vector functions behave like individual vectors, you can manipulate them the same way you can a vector. Vector calculus is used extensively throughout physics and engineering, mostly with regard to electromagnetic fields, gravitational fields, and fluid flow. When taking the derivative of a vector function, the function should be treated as a group of individual functions.

Vector functions are used in a number of differential operations, such as gradient (measures the rate and direction of change in a scalar field), curl (measures the tendency of the vector function to rotate about a point in a vector field), and divergence (measures the magnitude of a source at a given point in a vector field).