Arc Curvature
The curvature of an arc is a value that represents the direction and sharpness of a curve . On any curve, there is a center of curvature, C. This is the intersection point of two infinitely close normals to this curve. The radius, R, is the distance from this intersection point to the center of curvature.
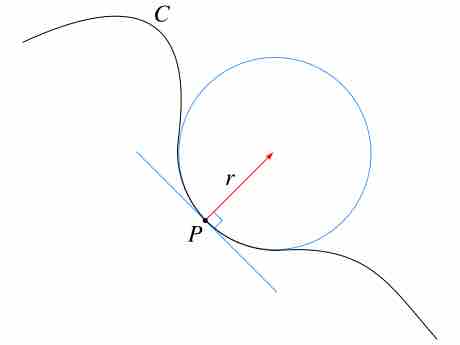
Curvature
Curvature is the amount an object deviates from being flat. Given any curve C and a point P on it, there is a unique circle or line which most closely approximates the curve near P\. The curvature of C at P is then defined to be the curvature of that circle or line. The radius of curvature is defined as the reciprocal of the curvature.
In order to find the value of the curvature, we need to take the parameter time, s, and the unit tangent vector, which in this case is the same as the unit velocity vector, T, which is also a function of time.The curvature is a magnitude of the rate of change of the tangent vector, T:
Where
How Does This Relate to Arc Length?
The curvature can also be approximated using limits. Given the points P and Q on the curve, lets call the arc length s(P,Q), and the linear distance from P to Q will be denoted as d(P,Q). The curvature of the arc at point P can be found by obtaining the limit:
In order to use this formula, you must first obtain the arc length of the curve from points P to Q and length of the linear segment that connect points P and Q. In a previous atom, we went into more detail on how to find the arc length, but for the sake of this atom we will just restate those formulas:In Cartesian coordinates: