Triple Integrals in Spherical Coordinates

When the function to be integrated has a spherical symmetry, it is sensible to change the variables into spherical coordinates and then perform integration.

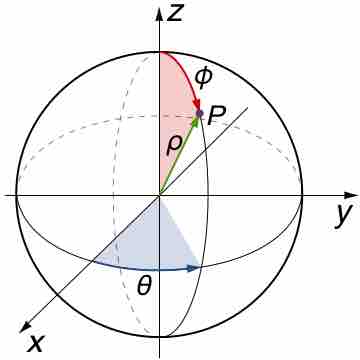
Spherical Coordinates

Spherical coordinates are useful when domains in $R^3$ have spherical symmetry.

In $R^3$ some domains have a spherical symmetry, so it's possible to specify the coordinates of every point of the integration region by two angles and one distance. It's possible to use therefore the passage in spherical coordinates; the function is transformed by this relation: 

$f(x,y,z) \longrightarrow f(\rho \cos \theta \sin \varphi, \rho \sin \theta \sin \varphi, \rho \cos \varphi)$

Points on $z$-axis do not have a precise characterization in spherical coordinates, so $\theta$ can vary from $0$ to $2 \pi$. The better integration domain for this passage is obviously the sphere.

Integrals in Spherical Coordinates

The Jacobian determinant of this transformation is the following: 

$\displaystyle{\frac{\partial (x,y,z)}{\partial (\rho, \theta, \varphi)}} = \begin{vmatrix} \cos \theta \sin \varphi & - \rho \sin \theta \sin \varphi & \rho \cos \theta \cos \varphi \\ \sin \theta \sin \varphi & \rho \cos \theta \sin \varphi & \rho \sin \theta \cos \varphi \\ \cos \varphi & 0 & - \rho \sin \varphi \end{vmatrix} = \rho^2 \sin \varphi$

The $dx\, dy\, dz$ differentials therefore are transformed to $\rho^2 \sin \varphi \, d\rho \,d\varphi \,dz$.

Finally, you obtain the final integration formula: It's better to use this method in case of spherical domains and in case of functions that can be easily simplified, by the first fundamental relation of trigonometry, extended in $R^3$; in other cases it can be better to use cylindrical coordinates.

Example

Integrate $f(x,y,z) = x^2 + y^2 + z^2$ over the domain $D = x^2 + y^2 + z^2 \le 16$. 

In spherical coordinates: 

$f(\rho \sin \varphi \cos \theta, \rho \sin \varphi \sin \theta, \rho \cos \varphi) = \rho^2$

while the intervals of the transformed region $T$ from $D$:

$0 \leq \rho \leq 4, 0 \leq \varphi \leq \pi, 0 \leq \theta \leq 2\pi$

Therefore:

$\begin{aligned} \iiint_D (x^2 + y^2 +z^2) \, dx\, dy\, dz &= \iiint_T \rho^2 \ \rho^2 \sin \theta \, d\rho\, d\theta\, d\phi, \\ &= \int_0^{\pi} \sin \phi \,d\phi \int_0^4 \rho^4 d \rho \int_0^{2 \pi} d\theta \\ &= 2 \pi \int_0^{\pi} \sin \phi \left[ \frac{\rho^5}{5} \right]_0^4 \, d \phi \\ &= 2 \pi \left[ \frac{\rho^5}{5} \right]_0^4 \left[- \cos \phi \right]_0^{\pi}= \frac{4096 \pi}{5} \end{aligned}$