In
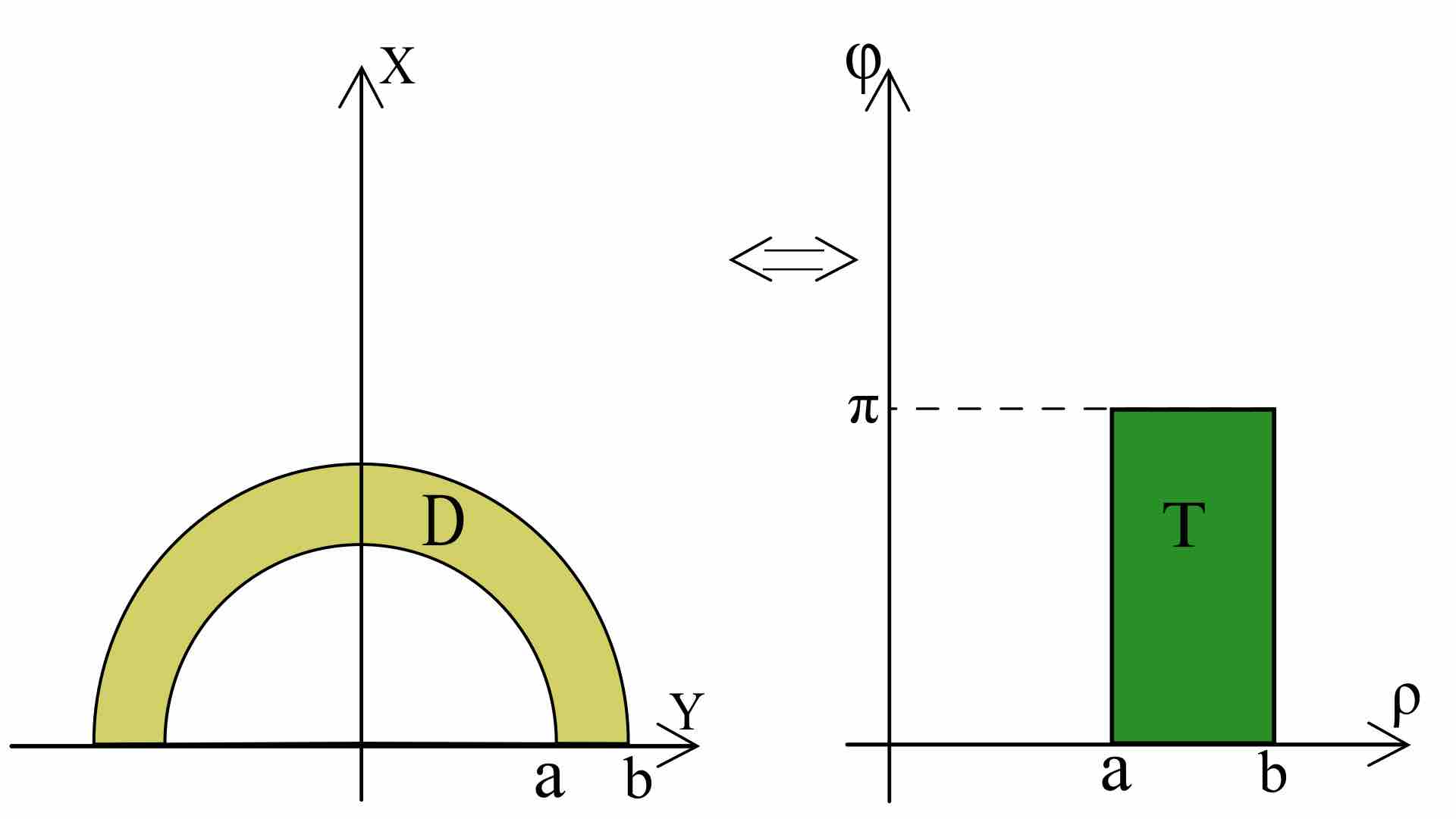
Transformation to Polar Coordinates
This figure illustrates graphically a transformation from cartesian to polar coordinates
Change of variable
The polar coordinates
The Cartesian coordinates
The fundamental relation to make the transformation is as follows:
Examples
- Given the function
$f(x,y) = x + y$ and applying the transformation, one obtains$f(\rho, \phi) = \rho \cos \phi + \rho \sin \phi = \rho(\cos \phi + \sin \phi )$ . - Given the function
$f(x,y) = x^2 + y^2$ , one can obtain$f(\rho, \phi) = \rho^2 (\cos^2 \phi + \sin^2 \phi) = \rho^2$ using the Pythagorean trigonometric identity, which is very useful to simplify this operation. Particularly in this case, you can see that the representation of the function f became simpler in polar coordinates. This is the case because the function has a cylindrical symmetry. In general, the best practice is to use the coordinates that match the built-in symmetry of the function.
Integrals in Polar Coordinates
The Jacobian determinant of that transformation is the following:
which has been obtained by inserting the partial derivatives of
Example
Integrate the function
From