The limits of integration are often not easily interchangeable (without normality or with complex formulae to integrate). One makes a change of variables to rewrite the integral in a more "comfortable" region, which can be described in simpler formulae. To do so, the function must be adapted to the new coordinates.
For example, for the function
which is simpler than the original form. When changing integration variables, however, make sure that the integral domain also changes accordingly. In the example, if integration is performed over
1. Polar coordinates
The function to be integrated transforms as:
and the integral accordingly changes as:
2. Cylindrical coordinates
The function to be integrated transforms as:
and the integral accordingly changes as:
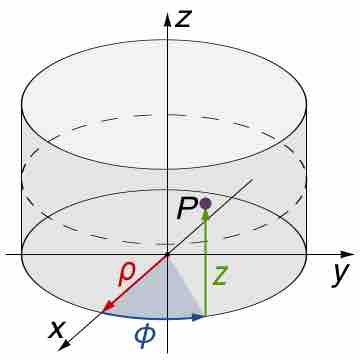
Cylindrical Coordinates
Changing to cylindrical coordinates may be useful depending on the setup of problem.
3. Spherical coordinates
The function to be integrated transforms as:
and the integral accordingly changes as: