Numbers and Operations

The basic arithmetic operations for real numbers are addition, subtraction, multiplication, and division.

Arithmetic operations can be performed on negative numbers according to specific rules.

A fraction represents a part of a whole and consists of an integer numerator and a non-zero integer denominator.

A complex fraction is one in which the numerator, denominator, or both are fractions, which can contain variables, constants, or both.

Exponential form, written $b^n$, represents multiplying the base $b$ times itself $n$ times.

The order of operations is an approach to evaluating expressions that involve multiple arithmetic operations.

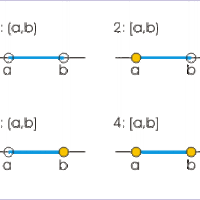
Interval notation uses parentheses and brackets to describe sets of real numbers and their endpoints.

Absolute value can be thought of as the distance of a real number from zero.

A set is a collection of unique numbers, often denoted with curly brackets: {}.

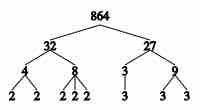
Any whole number greater than one can be factored, which means it can be broken down into smaller integers.

Percentages are used to express how large or small one quantity is relative to another quantity.

The arithmetic mean, or average, of a set of numbers indicates the "middle" or "typical" value of a data set.

Radical expressions yield roots and are the inverse of exponential expressions.

Radicals and exponents have particular requirements for addition and subtraction while multiplication is carried out more freely.

Root rationalization is a process by which any roots in the denominator of an irrational fraction are eliminated.

There is no such value such that when squared it results in a negative value; we therefore classify roots of negative numbers as "imaginary."

There are rules for operating on numbers with exponents that make it easy to simplify and solve problems.

Numbers with negative exponents are treated normally in arithmetic operations and can be rewritten as fractions.

Rational exponents are another method for writing radicals and can be used to simplify expressions involving both exponents and roots.

Scientific notation is used to express a very large or small number in the form $m \cdot 10^n$, where $m$ has only one digit left of the decimal point.