Information

Information as a concept bears a diversity of meanings, from everyday usage to technical settings. Generally speaking, the concept of information is closely related to notions of constraint, communication, control, data, form, instruction, knowledge, meaning, mental stimulus, pattern, perception, and representation.

Many people speak about the Information Age as the advent of the Knowledge Age or knowledge society, the information society, and information technologies, and even though informatics, information science and computer science are often in the spotlight, the word "information" is often used without careful consideration of the various meanings it has acquired.

Etymology

According to the Oxford English Dictionary, the earliest historical meaning of the word information in English was the act of informing, or giving form or shape to the mind, as in education, instruction, or training. A quote from 1387: "Five books come down from heaven for information of mankind." It was also used for an item of training, e.g. a particular instruction. "Melibee had heard the great skills and reasons of Dame Prudence, and her wise information and techniques." (1386)

The English word was apparently derived by adding the common "noun of action" ending "-ation" (descended through French from Latin "-tio") to the earlier verb to inform, in the sense of to give form to the mind, to discipline, instruct, teach: "Men so wise should go and inform their kings." (1330) Inform itself comes (via French) from the Latin verb informare, to give form to, to form an idea of. Furthermore, Latin itself already even contained the word informatio meaning concept or idea, but the extent to which this may have influenced the development of the word information in English is unclear.

As a final note, the ancient Greek word for form was eidos, and this word was famously used in a technical philosophical sense by Plato (and later Aristotle) to denote the ideal identity or essence of something (see Theory of forms). "Eidos" can also be associated with thought, proposition or even concept.

Information as a message

Information is the state of a system of interest. Message is the information materialized.

Information is a quality of a message from a sender to one or more receivers. Information is always about something (size of a parameter, occurrence of an event, etc). Viewed in this manner, information does not have to be accurate. It may be a truth or a lie, or just the sound of a kiss. Even a disruptive noise used to inhibit the flow of communication and create misunderstanding would in this view be a form of information. However, generally speaking, if the amount of information in the received message increases, the message is more accurate.

This model assumes there is a definite sender and at least one receiver. Many refinements of the model assume the existence of a common language understood by the sender and at least one of the receivers. An important variation identifies information as that which would be communicated by a message if it were sent from a sender to a receiver capable of understanding the message. However, in requiring the existence of a definite sender, the "information as a message" model does not attach any significance to the idea that information is something that can be extracted from an environment, e.g., through observation, reading or measurement.

Information is a term with many meanings depending on context, but is as a rule closely related to such concepts as meaning, knowledge, instruction, communication, representation, and mental stimulus. Simply stated, information is a message received and understood. In terms of data, it can be defined as a collection of facts from which conclusions may be drawn. There are many other aspects of information since it is the knowledge acquired through study or experience or instruction. But overall, information is the result of processing, manipulating and organizing data in a way that adds to the knowledge of the person receiving it.

Communication theory is a numerical measure of the uncertainty of an outcome. For example, we can say that "the signal contained thousands of bits of information". Communication theory tends to use the concept of information entropy, generally attributed to C.E. Shannon (see below).

Another form of information is Fisher information, a concept of R.A. Fisher. This is used in application of statistics to estimation theory and to science in general. Fisher information is thought of as the amount of information that a message carries about an unobservable parameter. It can be computed from knowledge of the likelihood function defining the system. For example, with a normal likelihood function, the Fisher information is the reciprocal of the variance of the law. In the absence of knowledge of the likelihood law, the Fisher information may be computed from normally distributed score data as the reciprocal of their second moment.

Even though information and data are often used interchangeably, they are actually very different. Data is a set of unrelated information, and as such is of no use until it is properly evaluated. Upon evaluation, once there is some significant relation between data, and they show some relevance, then they are converted into information. Now this same data can be used for different purposes. Thus, till the data convey some information, they are not useful.

Measuring information entropy

The view of information as a message came into prominence with the publication in 1948 of an influential paper by Claude Shannon, " A Mathematical Theory of Communication." This paper provides the foundations of information theory and endows the word information not only with a technical meaning but also a measure. If the sending device is equally likely to send any one of a set of 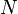messages, then the preferred measure of "the information produced when one message is chosen from the set" is the base two logarithm of (This measure is called self-information). In this paper, Shannon continues:

The choice of a logarithmic base corresponds to the choice of a unit for measuring information. If the base 2 is used the resulting units may be called binary digits, or more briefly bits, a word suggested by J. W. Tukey. A device with two stable positions, such as a relay or a flip-flop circuit, can store one bit of information. N such devices can store N bits…

A complementary way of measuring information is provided by algorithmic information theory. In brief, this measures the information content of a list of symbols based on how predictable they are, or more specifically how easy it is to compute the list through a program: the information content of a sequence is the number of bits of the shortest program that computes it. The sequence below would have a very low algorithmic information measurement since it is a very predictable pattern, and as the pattern continues the measurement would not change. Shannon information would give the same information measurement for each symbol, since they are statistically random, and each new symbol would increase the measurement.

123456789101112131415161718192021

It is important to recognize the limitations of traditional information theory and algorithmic information theory from the perspective of human meaning. For example, when referring to the meaning content of a message Shannon noted “Frequently the messages have meaning… these semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages” (emphasis in original).

In information theory signals are part of a process, not a substance; they do something, they do not contain any specific meaning. Combining algorithmic information theory and information theory we can conclude that the most random signal contains the most information as it can be interpreted in any way and cannot be compressed.

Micheal Reddy noted that "'signals' of the mathematical theory are 'patterns that can be exchanged'. There is no message contained in the signal, the signals convey the ability to select from a set of possible messages." In information theory "the system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design".

Information as a pattern

Information is any represented pattern. This view assumes neither accuracy nor directly communicating parties, but instead assumes a separation between an object and its representation. Consider the following example: economic statistics represent an economy, however inaccurately. What are commonly referred to as data in computing, statistics, and other fields, are forms of information in this sense. The electro-magnetic patterns in a computer network and connected devices are related to something other than the pattern itself, such as text characters to be displayed and keyboard input. Signals, signs, and symbols are also in this category. On the other hand, according to semiotics, data is symbols with certain syntax and information is data with a certain semantic. Painting and drawing contain information to the extent that they represent something such as an assortment of objects on a table, a profile, or a landscape. In other words, when a pattern of something is transposed to a pattern of something else, the latter is information. This would be the case whether or not there was anyone to perceive it.

But if information can be defined merely as a pattern, does that mean that neither utility nor meaning are necessary components of information? Arguably a distinction must be made between raw unprocessed data and information which possesses utility, value or some quantum of meaning. On this view, information may indeed be characterized as a pattern; but this is a necessary condition, not a sufficient one.

An individual entry in a telephone book, which follows a specific pattern formed by name, address and telephone number, does not become "informative" in some sense unless and until it possesses some degree of utility, value or meaning. For example, someone might look up a girlfriend's number, might order a take away etc. The vast majority of numbers will never be construed as "information" in any meaningful sense. The gap between data and information is only closed by a behavioural bridge whereby some value, utility or meaning is added to transform mere data or pattern into information.

When one constructs a representation of an object, one can selectively extract from the object ( sampling) or use a system of signs to replace ( encoding), or both. The sampling and encoding result in representation. An example of the former is a "sample" of a product; an example of the latter is "verbal description" of a product. Both contain information of the product, however inaccurate. When one interprets representation, one can predict a broader pattern from a limited number of observations (inference) or understand the relation between patterns of two different things ( decoding). One example of the former is to sip a soup to know if it is spoiled; an example of the latter is examining footprints to determine the animal and its condition. In both cases, information sources are not constructed or presented by some "sender" of information. Regardless, information is dependent upon, but usually unrelated to and separate from, the medium or media used to express it. In other words, the position of a theoretical series of bits, or even the output once interpreted by a computer or similar device, is unimportant, except when someone or something is present to interpret the information. Therefore, a quantity of information is totally distinct from its medium.

Information as sensory input

Often information is viewed as a type of input to an organism or designed device. Inputs are of two kinds. Some inputs are important to the function of the organism (for example, food) or device (energy) by themselves. In his book Sensory Ecology, Dusenbery called these causal inputs. Other inputs (information) are important only because they are associated with causal inputs and can be used to predict the occurrence of a causal input at a later time (and perhaps another place). Some information is important because of association with other information but eventually there must be a connection to a causal input. In practice, information is usually carried by weak stimuli that must be detected by specialized sensory systems and amplified by energy inputs before they can be functional to the organism or device. For example, light is often a causal input to plants but provides information to animals. The colored light reflected from a flower is too weak to do much photosynthetic work but the visual system of the bee detects it and the bee's nervous system uses the information to guide the bee to the flower, where the bee often finds nectar or pollen, which are causal inputs, serving a nutritional function.

Information is any type of sensory input. When an organism with a nervous system receives an input, it transforms the input into an electrical signal. This is regarded information by some. The idea of representation is still relevant, but in a slightly different manner. That is, while abstract painting does not represent anything concretely, when the viewer sees the painting, it is nevertheless transformed into electrical signals that create a representation of the painting. Defined this way, information does not have to be related to truth, communication, or representation of an object. Entertainment in general is not intended to be informative. Music, the performing arts, amusement parks, works of fiction and so on are thus forms of information in this sense, but they are not necessarily forms of information according to some definitions given above. Consider another example: food supplies both nutrition and taste for those who eat it. If information is equated to sensory input, then nutrition is not information but taste is.

Information as an influence which leads to a transformation

Information is any type of pattern that influences the formation or transformation of other patterns. In this sense, there is no need for a conscious mind to perceive, much less appreciate, the pattern. Consider, for example, DNA. The sequence of nucleotides is a pattern that influences the formation and development of an organism without any need for a conscious mind. Systems theory at times seems to refer to information in this sense, assuming information does not necessarily involve any conscious mind, and patterns circulating (due to feedback) in the system can be called information. In other words, it can be said that information in this sense is something potentially perceived as representation, though not created or presented for that purpose.

When Marshall McLuhan speaks of media and their effects on human cultures, he refers to the structure of artifacts that in turn shape our behaviors and mindsets. Also, pheromones are often said to be "information" in this sense.

(See also Gregory Bateson.)

Information as a property in physics

In 2003, J. D. Bekenstein claimed there is a growing trend in physics to define the physical world as being made of information itself (and thus information is defined in this way). Information has a well defined meaning in physics. Examples of this include the phenomenon of quantum entanglement where particles can interact without reference to their separation or the speed of light. Information itself cannot travel faster than light even if the information is transmitted indirectly. This could lead to the fact that all attempts at physically observing a particle with an "entangled" relationship to another are slowed down, even though the particles are not connected in any other way other than by the information they carry.

Another link is demonstrated by the Maxwell's demon thought experiment. In this experiment, a direct relationship between information and another physical property, entropy, is demonstrated. A consequence is that it is impossible to destroy information without increasing the entropy of a system; in practical terms this often means generating heat. Thus, in the study of logic gates, the theoretical lower bound of thermal energy released by an AND gate is higher than for the NOT gate (because information is destroyed in an AND gate and simply converted in a NOT gate). Physical information is of particular importance in the theory of quantum computers.

Information as records

Records are a specialized form of information. Essentially, records are information produced consciously or as by-products of business activities or transactions and retained because of their value. Primarily their value is as evidence of the activities of the organization but they may also be retained for their informational value. Sound records management ensures that the integrity of records is preserved for as long as they are required.

The international standard on records management, ISO 15489, defines records as "information created, received, and maintained as evidence and information by an organization or person, in pursuance of legal obligations or in the transaction of business". The International Committee on Archives (ICA) Committee on electronic records defined a record as, "a specific piece of recorded information generated, collected or received in the initiation, conduct or completion of an activity and that comprises sufficient content, context and structure to provide proof or evidence of that activity".

Records may be retained because of their business value, as part of the corporate memory of the organization or to meet legal, fiscal or accountability requirements imposed on the organization. Willis (2005) expressed the view that sound management of business records and information delivered "…six key requirements for good corporate governance…transparency; accountability; due process; compliance; meeting statutory and common law requirements; and security of personal and corporate information."