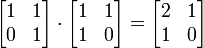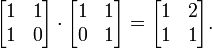Commutative ring
Background to the schools Wikipedia
This Schools selection was originally chosen by SOS Children for schools in the developing world without internet access. It is available as a intranet download. Sponsoring children helps children in the developing world to learn too.
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation obeys the commutative law. This means that if a and b are any elements of the ring, then a×b=b×a.
The study of commutative rings is called commutative algebra.
Examples
- The most important example is the ring of integers with the two operations of addition and multiplication. Ordinary multiplication of integers is commutative. This ring is usually denoted Z in the literature to signify the German word Zahlen (numbers).
- The rational, real and complex numbers form commutative rings; in fact, they are even fields.
- More generally, every field is a commutative ring, so the class of fields is a subclass of the class of commutative rings.
- A simple example of a non-commutative ring is the set of all 2-by-2 matrices whose entries are real numbers. For example, the matrix multiplication
-
- is not equal to the multiplication performed in the opposite order:
- If n is a positive integer, then the set Zn of integers modulo n forms a commutative ring with n elements (see modular arithmetic).
- If R is a given commutative ring, then the set of all polynomials in the variable X whose coefficients are in R forms a new commutative ring, denoted R[X].
- Similarly, the set of formal power series R[[X1,...,Xn]] over a commutative ring R is a commutative ring. If R is a field, the formal power series ring is a special kind of commutative ring, called a complete local ring.
- The set of all ordinary rational numbers whose denominator is odd forms a commutative ring, in fact a local ring. This ring contains the ring of integers properly, and is itself a proper subset of the rational field.
- If p is any prime number, the set of p-adic integers forms a commutative ring.
- A set of matrices that can be diagonalized with the same similarity transformation forms a commutative ring. An example is the set of matrices of divided differences with respect to a fixed set of nodes.
Constructing commutative rings
Given a commutative ring, one can use it to construct new rings, as described below.
- Factor ring: Given a commutative ring R and an ideal I of R, the factor ring R/I is the set of cosets of I together with the operations (a+I)+(b+I)=(a+b)+I and (a+I)(b+I)=ab+I.
- Localization: If S is a multiplicative subset of a commutative ring R then we can define the localization of R at S, or ring of fractions with denominators in S, usually denoted S-1R. The penultimate example above is the localization of the ring of integers at the multiplicative subset of odd integers. The field of rationals is the localization of the commutative ring of integers at the multiplicative set of non-zero integers.
- Completion: If I is an ideal in a commutative ring R, the powers of I form topological neighborhoods of 0 which allow R to be viewed as a topological ring. This topology is called the I-adic topology. R can then be completed with respect to this topology. Formally, the I-adic completion is the inverse limit of the rings R/In. For example, if k is a field, k[[X]], the formal power series ring in one variable over k, is the I-adic completion of k[X] where I is the principal ideal generated by X. Analogously, the ring of p-adic integers is the I-adic completion of Z where I is the principal ideal generated by p.
- If R is a given commutative ring, the set of all polynomials R[X1,...,Xn] over R forms a new commutative ring, called the polynomial ring in n variables over R.
- If Ris a given commutative ring, then the set of all formal power series R[[X1,...,Xn]] over a commutative ring R is a commutative ring, called the power series ring in n variables over R.
Properties
- All subrings and quotient rings of commutative rings are also commutative.
- If f : R → S is an injective ring homomorphism (that is, a monomorphism) between rings R and S, and if S is commutative, then R must also be commutative, since f(a·b) = f(a)·f(b) = f(b)·f(a) = f(b·a).
- Similarly, if f : R → S is a ring homomorphism between rings R and S, and if R is commutative, the subring f(R) of S is also commutative; in particular, if f is surjective (and therefore an epimorphism), S must be commutative.
- Every finite division ring is commutative ( Wedderburn's theorem). N. Jacobson has shown that the following condition is sufficient: if R is a ring such that for every element x of R there exists an integer n > 1 such that xn = x, then R is commutative. Much more general conditions which guarantee commutativity of a ring were subsequently discovered by I. N. Herstein and others.
General discussion
The inner structure of a commutative ring is determined by considering its ideals. All ideals in a commutative ring are two-sided, which simplifies the situation considerably.
The outer structure of a commutative ring is determined by considering linear algebra over that ring, i.e., by investigating the theory of its modules. This subject is significantly more difficult when the commutative ring is not a field and is usually called homological algebra. The set of ideals within a commutative ring R can be exactly characterized as the set of R-modules which are submodules of R.
An element a of a commutative ring (with identity) is called a unit if it possesses a multiplicative inverse, i.e., if there exists another element b of the ring (with b not necessarily distinct from a) so that ab = 1. Every nonzero element of a field is a unit. Every element of a commutative local ring not contained in the maximal ideal is a unit.
A non-zero element a of a commutative ring is said to be a zero divisor if there exists a non-zero element b of the ring such that ab = 0. A commutative ring with identity which possesses no zero divisors is called an integral domain since it closely resembles the integers in some ways.
Some specific kinds of commutative rings are given with the following chain of inclusions:
commutative rings ⊃ integral domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields
Another possible chain (which is more geometric) is the following chain of inclusions:
Cohen-Macaulay rings ⊃ Gorenstein rings ⊃ Regular rings ⊃ Regular local rings