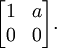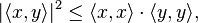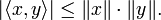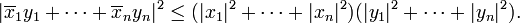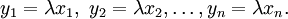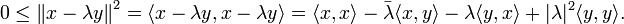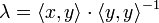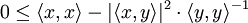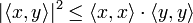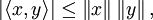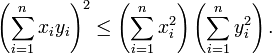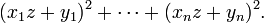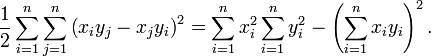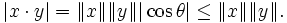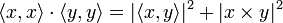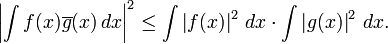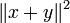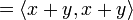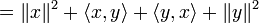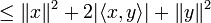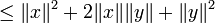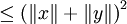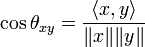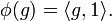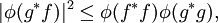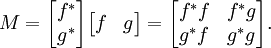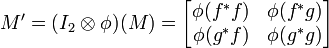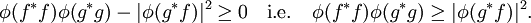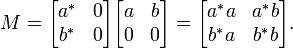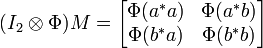Cauchy–Schwarz inequality
Background to the schools Wikipedia
This wikipedia selection has been chosen by volunteers helping SOS Children from Wikipedia for this Wikipedia Selection for schools. A good way to help other children is by sponsoring a child
In mathematics, the Cauchy–Schwarz inequality, also known as the Schwarz inequality, the Cauchy inequality, or the Cauchy–Bunyakovsky–Schwarz inequality, is a useful inequality encountered in many different settings, such as linear algebra applied to vectors, in analysis applied to infinite series and integration of products, and in probability theory, applied to variances and covariances.
The inequality for sums was published by Augustin Cauchy (1821), while the corresponding inequality for integrals was first stated by Viktor Yakovlevich Bunyakovsky (1859) and rediscovered by Hermann Amandus Schwarz (1888) (often misspelled "Schwartz").
Statement of the inequality
The Cauchy–Schwarz inequality states that for all vectors x and y of a real or complex inner product space,
where 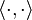 is the inner product. Equivalently, by taking the square root of both sides, and referring to the norms of the vectors, the inequality is written as
is the inner product. Equivalently, by taking the square root of both sides, and referring to the norms of the vectors, the inequality is written as
Moreover, the two sides are equal if and only if 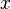 and
and 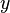 are linearly dependent (or, in a geometrical sense, they are parallel or one of the vectors is equal to zero).
are linearly dependent (or, in a geometrical sense, they are parallel or one of the vectors is equal to zero).
If 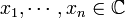 and
and 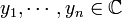 are the components of
are the components of 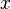 and
and 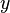 with respect to an orthonormal basis of
with respect to an orthonormal basis of 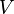 the inequality may be restated in a more explicit way as follows:
the inequality may be restated in a more explicit way as follows:
Equality holds if and only if either 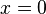 , or there exists a scalar
, or there exists a scalar 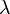 such that
such that
The finite-dimensional case of this inequality for real vectors was proved by Cauchy in 1821, and in 1859 Cauchy's student V.Ya. Bunyakovsky noted that by taking limits one can obtain an integral form of Cauchy's inequality. The general result for an inner product space was obtained by K.H.A.Schwarz in 1885.
Proof
As the inequality is trivially true in the case y = 0, we may assume <y, y> is nonzero. Let 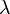 be a complex number. Then,
be a complex number. Then,
Choosing
we obtain
which is true if and only if
or equivalently:
which is the Cauchy–Schwarz inequality.
Notable special cases
Rn
In Euclidean space Rn with the standard inner product, the Cauchy–Schwarz inequality is
In this special case, an alternative proof is as follows: Consider the polynomial in z
Note that the polynomial is quadratic in z. Since the polynomial is nonnegative, it cannot have any roots unless all the ratios xi/yi are equal. Hence its discriminant is less than or equal to zero, that is,
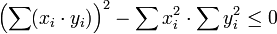 ,
,
which yields the Cauchy–Schwarz inequality.
An equivalent proof for Rn starts with the summation below.
Expanding the brackets we have:
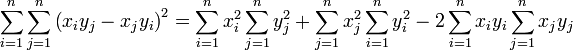 ,
,
collecting together identical terms (albeit with different summation indices) we find:
Because the left-hand side of the equation is a sum of the squares of real numbers it is greater than or equal to zero, thus:
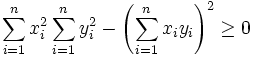 .
.
Also, when n = 2 or 3, the dot product is related to the angle between two vectors and one can immediately see the inequality:
Furthermore, in this case the Cauchy–Schwarz inequality can also be deduced from Lagrange's identity. For n = 3, Lagrange's identity takes the form
from which readily follows the Cauchy–Schwarz inequality.
L2
For the inner product space of square-integrable complex-valued functions, one has
A generalization of this is the Hölder inequality.
Use
The triangle inequality for the inner product is often shown as a consequence of the Cauchy–Schwarz inequality, as follows: given vectors x and y,
Taking the square roots gives the triangle inequality.
The Cauchy–Schwarz inequality allows one to extend the notion of "angle between two vectors" to any real inner product space, by defining:
The Cauchy–Schwarz inequality proves that this definition is sensible, by showing that the right hand side lies in the interval ![[-1,1]](../../images/144/14442.png) , and justifies the notion that real inner product spaces are simply generalizations of the Euclidean space.
, and justifies the notion that real inner product spaces are simply generalizations of the Euclidean space.
The Cauchy–Schwarz is used to prove that the inner product is a continuous function with respect to the topology induced by the inner product itself.
The Cauchy–Schwarz inequality is usually used to show Bessel's inequality.
The general formulation of the Heisenberg uncertainty principle is derived using the Cauchy–Schwarz inequality in the inner product space of physical wave functions.
Generalizations
Various generalizations of the Cauchy–Schwarz inequality exist in the context of operator theory, e.g. for operator-convex functions, and operator algebras, where the domain and/or range of φ are replaced by a C*-algebra or W*-algebra.
This section lists a few of such inequalities from the operator algebra setting, to give a flavor of results of this type.
Positive functionals on C*- and W*-algebras
One can discuss inner products as positive functionals. Given a Hilbert space L2(m), m being a finite measure, the inner product < · , · > gives rise to a positive functional φ by
Since < f,f > ≥ 0, φ(f*f) ≥ 0 for all f in L2(m), where f* is pointwise conjugate of f. So φ is positive. Conversely every positive functional φ gives a corresponding inner product < f , g >φ = φ(g*f). In this language, the Cauchy–Schwarz inequality becomes
which extends verbatim to positive functionals on C*-algebras.
We now give an operator theoretic proof for the Cauchy–Schwarz inequality which passes to the C*-algebra setting. One can see from the proof that the Cauchy–Schwarz inequality is a consequence of the positivity and anti-symmetry inner-product axioms.
Consider the positive matrix
Since φ is a positive linear map whose range, the complex numbers C, is a commutative C*-algebra, φ is completely positive. Therefore
is a positive 2 × 2 scalar matrix, which implies it has positive determinant:
This is precisely the Cauchy–Schwarz inequality. If f and g are elements of a C*-algebra, f* and g* denote their respective adjoints.
We can also deduce from above that every positive linear functional is bounded, corresponding to the fact that the inner product is jointly continuous.
Positive maps
Positive functionals are special cases of positive maps. A linear map Φ between C*-algebras is said to be a positive map if a ≥ 0 implies Φ(a) ≥ 0. It is natural to ask whether inequalities of Schwarz-type exist for positive maps. In this more general setting, usually additional assumptions are needed to obtain such results.
Kadison's inequality
One such inequality is the following:
Theorem If Φ is a unital positive map, then for every normal element a in its domain, we have Φ(a*a) ≥ Φ(a*)Φ(a) and Φ(a*a) ≥ Φ(a)Φ(a*).
This extends the fact φ(a*a) · 1 ≥ φ(a)*φ(a) = |φ(a)|2, when φ is a linear functional.
The case when a is self-adjoint, i.e. a = a*, is known as Kadison's inequality.
2-positive maps
When Φ is 2-positive, a stronger assumption than merely positive, one has something that looks very similar to the original Cauchy–Schwarz inequality:
Theorem (Modified Schwarz inequality for 2-positive maps) For a 2-positive map Φ between C*-algebras, for all a, b in its domain,
- i) Φ(a)*Φ(a) ≤ ||Φ(1)|| Φ(a*a).
- ii) ||Φ(a*b)||2 ≤ ||Φ(a*a)|| · ||Φ(b*b)||.
A simple argument for ii) is as follows. Consider the positive matrix
By 2-positivity of Φ,
is positive. The desired inequality then follows from the properties of positive 2 × 2 (operator) matrices.
Part i) is analogous. One can replace the matrix 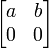 by
by