Age of the universe

About this schools Wikipedia selection

SOS Children volunteers helped choose articles and made other curriculum material Sponsor a child to make a real difference.

The age of the universe is the time elapsed between the Big Bang and the present day. Current observations suggest that this is about 13.73 billion years, with an uncertainty of about 120 million years.

Explanation

The Lambda-CDM concordance model describes the evolution of the universe from a very uniform, hot, dense primordial state to its present state over a span of about 13.7 billion years of cosmological time. This model is well understood theoretically and strongly supported by recent high-precision astronomical observations such as WMAP. In contrast, theories of the origin of the primordial state remain very speculative. The dominant theory, inflation, as well as the recent ekpyrotic scenario, suggest that the Big Bang cosmos that we observe may be a part of a larger universe with very different physical properties and with a history extending back longer than 13.7 billion years. It is not yet clear whether these ideas are testable, even in principle.

If one extrapolates the Lambda-CDM model backward from the earliest well-understood state, it quickly (within a small fraction of a second) reaches a mathematical singularity called the "Big Bang singularity." This singularity is not considered to have any physical significance, but it is convenient to quote times measured "since the Big Bang," even though they do not correspond to a physically measurable time. For example, "10⁻⁶ second after the Big Bang" is a well-defined era in the universe's evolution. In one sense it would be more meaningful to refer to the same era as "13.7 billion years minus 10⁻⁶ seconds ago," but this is unworkable since the latter time interval is swamped by uncertainty in the former.

Though the universe might in theory have a longer history, cosmologists presently use "age of the universe" to mean the duration of the Lambda-CDM expansion, or equivalently the elapsed time since the Big Bang.

Observational limits on the age of the universe

Since the universe must be at least as old as the oldest thing in it, there are a number of observations which put a lower limit on the age of the universe. These include the temperature of the coolest white dwarfs, and the turnoff point of the red dwarfs.

Age as a function of cosmological parameters

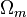The age of the universe can be determined by measuring the Hubble constant today and extrapolating back in time with the observed value of density parameters (Ω). Before the discovery of dark energy, it was believed that the universe was matter-dominated, and so Ω on this graph corresponds to $\Omega_m$ . Note that the accelerating universe has the greatest age, while the Big Crunch universe has the smallest age.

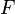The value of the age correction factor $F$ is shown as a function of two cosmological parameters: the current fractional matter density 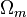$\Omega_m$ and cosmological constant density 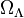$\Omega_\Lambda$ . The best-fit values of these parameters are shown by the box in the upper left; the matter-dominated universe is shown by the star in the lower right.

The problem of determining the age of the universe is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the Universe is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. 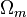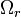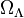The fractional contribution of each to the current energy density of the Universe is given by the density parameters $\Omega_m$ , $\Omega_r$ , and $\Omega_\Lambda$ . The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter 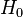$H_0$ are the most important.

If one has accurate measurements of these parameters, then the age of the universe can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor 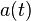$a(t)$ to the matter content of the Universe. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total age of the universe by integrating this formula. The age 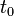$t_0$ is then given by an expression of the form, 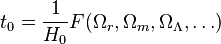$t_0 = \frac{1}{H_0} F(\Omega_r,\Omega_m,\Omega_\Lambda,\dots)$ where the function 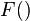$F()$ depends only on the fractional contribution to the Universe's energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls that age of the universe, with a correction arising from the matter and energy content. So a rough estimate of the age of the universe comes from the inverse of the Hubble parameter,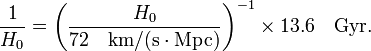 $\frac{1}{H_0} = \left( \frac{H_0}{72\quad\text{km/(s}\cdot\text{Mpc)} } \right)^{-1} \times 13.6 \quad\text{Gyr}.$

To get a more accurate number, the correction factor $F()$ must be computed. In general this must be done numerically, and the results for a range of cosmological parameter values are shown in the figure. For the WMAP values ( $\Omega_m$ , $\Omega_\Lambda$ ) = (0.266,0.732), shown by the box in the upper left corner of the figure, this correction factor is nearly one: 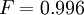$F=0.996$ . For a flat universe without any cosmological constant, shown by the star in the lower right corner, 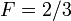$F = 2/3$ is much smaller and thus the universe is younger for a fixed value of the Hubble parameter. To make this figure, 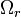$\Omega_r$ is held constant (roughly equivalent to holding the CMB temperature constant) and the curvature density parameter is fixed by the value of the other three.

The Wilkinson Microwave Anisotropy Probe ( WMAP) was instrumental in establishing an accurate age of the Universe, though other measurements must be folded in to gain an accurate number. CMB measurements are very good at constraining the matter content 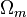$\Omega_m$ and curvature parameter 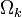$\Omega_k$ . It is not as sensitive to 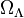$\Omega_\Lambda$ directly, partly because the cosmological constant only becomes important at low redshift. The most accurate determinations of the Hubble parameter 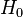$H_0$ come from Type Ia supernovae. Combining these measurements leads to the generally accepted value for the age of the universe quoted above.

The cosmological constant makes the universe "older" for fixed values of the other parameters. This is significant, since before the cosmological constant became generally accepted, the Big Bang model had difficulty explaining why globular clusters in the Milky Way appeared to be far older than the age of the universe as calculated from the Hubble parameter and a matter-only universe. Introducing the cosmological constant allows the universe to be older than these clusters, as well as explaining other features that the matter-only cosmological model could not.

Age based on WMAP

NASA's Wilkinson Microwave Anisotropy Probe (WMAP) project estimates the age of the universe to be:

(13.73 ± 0.12) × 10⁹ years.

That is, the universe is about 13.73 billion years old, with an uncertainty of 120 million years. However, this age is based on the assumption that the project's underlying model is correct; other methods of estimating the age of the universe could give different ages. Assuming an extra background of relativistic particles, for example, can enlarge the error bars of the WMAP constraint by one order of magnitude.

This measurement is made by using the location of the first acoustic peak in the microwave background power spectrum to determine the size of the decoupling surface (size of universe at the time of recombination). The light travel time to this surface (depending on the geometry used) yields a reliable age for the universe. Assuming the validity of the models used to determine this age, the residual accuracy yields a margin of error near one percent.

This is the value currently most quoted by astronomers.

Assumption of strong priors

Calculating the age of the universe is only accurate if the assumptions built into the models being used to estimate it are also accurate. This is referred to as strong priors and essentially involves stripping the potential errors in other parts of the model to render the accuracy of actual observational data directly into the concluded result. Although this is not a valid procedure in all contexts (as noted in the accompanying caveat: "based on the fact we have assumed the underlying model we used is correct"), the age given is thus accurate to the specified error (since this error represents the error in the instrument used to gather the raw data input into the model).

The age of the universe based on the "best fit" to WMAP data "only" is 13.69±0.13 Gyr (the slightly higher number of 13.73 includes some other data mixed in). This number represents the first accurate "direct" measurement of the age of the universe (other methods typically involve Hubble's law and age of the oldest stars in globular clusters, etc). It is possible to use different methods for determining the same parameter (in this case – the age of the universe) and arrive at different answers with no overlap in the "errors". To best avoid the problem, it is common to show two sets of uncertainties; one related to the actual measurement and the other related to the systematic errors of the model being used.

An important component to the analysis of data used to determine the age of the universe (e.g. from WMAP) therefore is to use a Bayesian Statistical analysis, which normalizes the results based upon the priors (i.e. the model). This quantifies any uncertainty in the accuracy of a measurement due to a particular model used.

Retrieved from " http://en.wikipedia.org/w/index.php?title=Age_of_the_universe&oldid=221149886"