Summary
| Description |
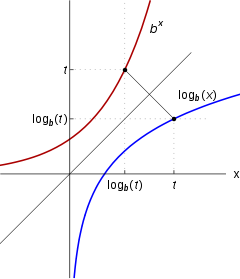
English: Logarithm function as the inverse of an exponential, shown on the same graph together with the 45° “mirror line”.
|
| Date |
4 March 2011 |
| Source |
Own work |
| Author |
Stpasha |
Source code in Mathematica
t = 3;
g2 = Plot[{Log[2, x], 2^x}, {x, -3, 5},
PlotRange -> {{-2, 4.5}, {-3, 5}}, AspectRatio -> 8/6.5,
ImageSize -> 240,
PlotStyle -> {{Thickness[0.007], Blue}, {Thickness[0.007],
Darker[Red]}},
AxesStyle ->
Directive[FontSize -> 12, FontFamily -> "Arial",
Thickness[0.003]],
AxesLabel -> {"x", None},
Ticks -> {{{Log[2, t], "\!\(\*SubscriptBox[\"log\", \"b\"]\)(\!\(\*
StyleBox[\"t\",\nFontSlant->\"Italic\"]\))"}, {t, "\!\(\*
StyleBox[\"t\",\nFontSlant->\"Italic\"]\)"}}, {{Log[2, t],
"\!\(\*SubscriptBox[\"log\", \"b\"]\)(\!\(\*
StyleBox[\"t\",\nFontSlant->\"Italic\"]\))"}, {t, "\!\(\*
StyleBox[\"t\",\nFontSlant->\"Italic\"]\)"}}},
Epilog -> {
Line[{{-2.3, -2.3}, {3.5, 3.5}}],
Line[{{t, Log[2, t]}, {Log[2, t], t}}],
Dotted, Gray,
Line[{{Log[2, t], 0}, {Log[2, t], 5}}],
Line[{{t, 0}, {t, Log[2, t]}}],
Line[{{0, Log[2, t]}, {4, Log[2, t]}}],
Line[{{0, t}, {Log[2, t], t}}],
Black, PointSize[Medium],
Point[{{t, Log[2, t]}, {Log[2, t], t}}],
FontSize -> 12, FontFamily -> "Arial",
Inset["\!\(\*SuperscriptBox[\"b\", \"x\"]\)", {2.5, 4.2}],
Inset[
"\!\(\*SubscriptBox[\"log\", \"b\"]\)\!\(\*AdjustmentBox[\"(\",\n\
BoxMargins->{{-0.12355212355212356`, 0.12355212355212356`}, {0., \
0.}}]\)\!\(\*AdjustmentBox[\"x\",\n\
BoxMargins->{{-0.12355212355212356`, 0.12355212355212356`}, {0., \
0.}}]\)\!\(\*AdjustmentBox[\")\",\n\
BoxMargins->{{-0.12355212355212356`, 0.12355212355212356`}, {0., \
0.}}]\)", {3.7, 2.3}]
}]
Export["Logarithm_inversefunctiontoexp.svg", g2]
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
  |
This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of his or her rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission. http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse
|
|
The following pages on Schools Wikipedia link to this image (list may be incomplete):