
File:Newton iteration.png
| |
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help. |
 |
File:Newton iteration.svg is a vector version of this file. It should be used in place of this raster image when superior. File:Newton iteration.png
For more information about vector graphics, read about Commons transition to SVG.
|
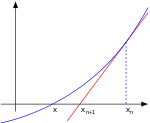 |
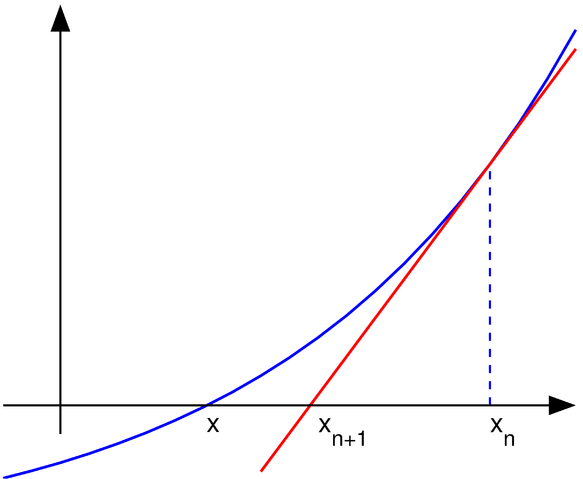
| Description | Uploader graphed this with en:MATLAB (Illustration of en:Newton's method) |
| Date | 22 November 2004 (first version); 2004-11-23 (last version) |
| Source | Originally from en.wikipedia; description page is/was here. |
| Author | Original uploader was Olegalexandrov at en.wikipedia |
| Permission ( Reusing this file) |
Released into the public domain (by the author). |
|
|
This chart was created with MATLAB. |
Licensing
| Public domainPublic domainfalsefalse |
 |
This work has been released into the public domain by its author, Olegalexandrov at the English Wikipedia project. This applies worldwide. In case this is not legally possible: |
Source code ( MATLAB)
% illustration of Newton's method for finding a zero of a function function main () a=-1; b=1; % interval endpoints fs=20; % text font size % arrows settings thickness1=2; thickness2=1.5; arrowsize=0.1; arrow_type=1; angle=20; % in degrees h=0.1; % grid size X=a:h:b; % points on the x axis f=inline('exp(x)/1.5-0.5'); % function to plot g=inline('exp(x)/1.5'); % derivative of f x0=0.7; y0=f(x0); % point at which to draw the tangent line m=g(x0); Y=f(X); % points on the function to plot XT=-0.1:h:b; YT=y0+(XT-x0)*m; % tangent line % prepare the screen clf; hold on; axis equal; axis off % plot the graph and the tangent lines plot(X, Y, 'linewidth', thickness1) plot(XT, YT, 'r', 'linewidth', thickness1) plot([x0 x0], [0, y0], '--', 'linewidth', thickness2) % axes small=0.2; arrow([a 0], [b, 0], thickness2, arrowsize, angle, arrow_type, [0, 0, 0]) arrow([a+small, -0.1], [a+small, 1.4], thickness2, arrowsize, angle, arrow_type, [0, 0, 0]) % text H=text(-0.29, -0.06, 'x'); set(H, 'fontsize', fs) H=text(0.1, -0.1, 'x_{n+1}'); set(H, 'fontsize', fs) H=text(0.7, -0.1, 'x_{n}'); set(H, 'fontsize', fs) % save to disk saveas(gcf, 'newton_iteration.eps', 'psc2') function arrow(start, stop, thickness, arrow_size, sharpness, arrow_type, colour) % Function arguments: % start, stop: start and end coordinates of arrow, vectors of size 2 % thickness: thickness of arrow stick % arrow_size: the size of the two sides of the angle in this picture -> % sharpness: angle between the arrow stick and arrow side, in degrees % arrow_type: 1 for filled arrow, otherwise the arrow will be just two segments % color: arrow colour, a vector of length three with values in [0, 1] % convert to complex numbers i=sqrt(-1); start=start(1)+i*start(2); stop=stop(1)+i*stop(2); rotate_angle=exp(i*pi*sharpness/180); % points making up the arrow tip (besides the "stop" point) point1 = stop - (arrow_size*rotate_angle)*(stop-start)/abs(stop-start); point2 = stop - (arrow_size/rotate_angle)*(stop-start)/abs(stop-start); if arrow_type==1 % filled arrow % plot the stick, but not till the end, looks bad t=0.5*arrow_size*cos(pi*sharpness/180)/abs(stop-start); stop1=t*start+(1-t)*stop; plot(real([start, stop1]), imag([start, stop1]), 'LineWidth', thickness, 'Colour', colour); % fill the arrow H=fill(real([stop, point1, point2]), imag([stop, point1, point2]), colour); set(H, 'EdgeColor', 'none') else % two-segment arrow plot(real([start, stop]), imag([start, stop]), 'LineWidth', thickness, 'Colour', colour); plot(real([stop, point1]), imag([stop, point1]), 'LineWidth', thickness, 'Colour', colour); plot(real([stop, point2]), imag([stop, point2]), 'LineWidth', thickness, 'Colour', colour); end
File usage
The best way to learn
Wikipedia for Schools was collected by SOS Childrens Villages. SOS Children is an international children's charity, providing a good home and loving family to thousands of children who have lost their parents. We also work with communities to help vulnerable families stay together and raise children in the best possible environment. You can help by sponsoring a child.
