12.2 Asset Bubbles

Asset bubblesIn this context, a rapid increase in asset prices that is not easily justified by fundamentals like expected earnings, interest rates, and the like. are rapid increases in the value of some asset, like bonds, commodities (cotton, gold, oil, tulips), equities, or real estate. Some combination of low interest rates, new technology, unprecedented increases in demand for the asset, and leverage typically create bubbles.

Low interest rates can cause bubbles by lowering the total cost of asset ownership. Recall from Chapter 4 "Interest Rates" that interest rates and bond prices are inversely related. Algebraically, the i term is in the denominator of the PV formula—PV = FV/(1 + i)ⁿ—so as it gets smaller, PV must get larger (holding FV constant, of course).

In 1762, Benjamin Franklin reported that the “Rent of old Houses, and Value of Lands, . . . are trebled in the last Six Years.”For more on the crisis, see Tim Arango, “The Housing-Bubble Revolution,” New York Times (30 November 2008), WK 5. http://www.nytimes.com/2008/11/30/weekinreview/30arango.html?_r=2&pagewanted=1&ref=weekinreview

The effect of new technology can be thought of as increasing FV, leading, of course, to a higher PV. Or, in the case of equities, low interest rates decrease k (required return) and new inventions increase g (constant growth rate) in the Gordon growth model—P = E × (1 + g)/(k – g)—both of which lead to a higher price.

Large increases in the demand for an asset occur for a variety of reasons. Demand can be increased merely by investors’ expectations of higher prices in the future, as in the one period valuation model—P = E/(1 + k) + P₁/(1 + k). If many investors believe that P₁ must be greater than P a year (or any other period) hence, demand for the asset will increase and the expectation of a higher P₁ will be vindicated. That sometimes leads investors to believe that P₂ will be higher than P₁, leading to a self-fulfilling cycle that repeats through P₃ to P_x. At some point, the value of the asset becomes detached from fundamental reality, driven solely by expectations of yet higher future prices. In fact, some scholars verify the existence of an asset bubble when news about the price of an asset affects the economy, rather than the economy affecting the price of the asset.

To increase their returns, investors often employ leverage, or borrowing. Compare three investors, one who buys asset X entirely with his own money, one who borrows half of the price of asset X, and one who borrows 90 percent of the price of asset X. Their returns (not including the cost of borrowing, which as noted above is usually low during bubbles) will be equal to those calculated in Figure 12.1 "The effects of leverage on returns in a rising market".

Figure 12.1 The effects of leverage on returns in a rising market

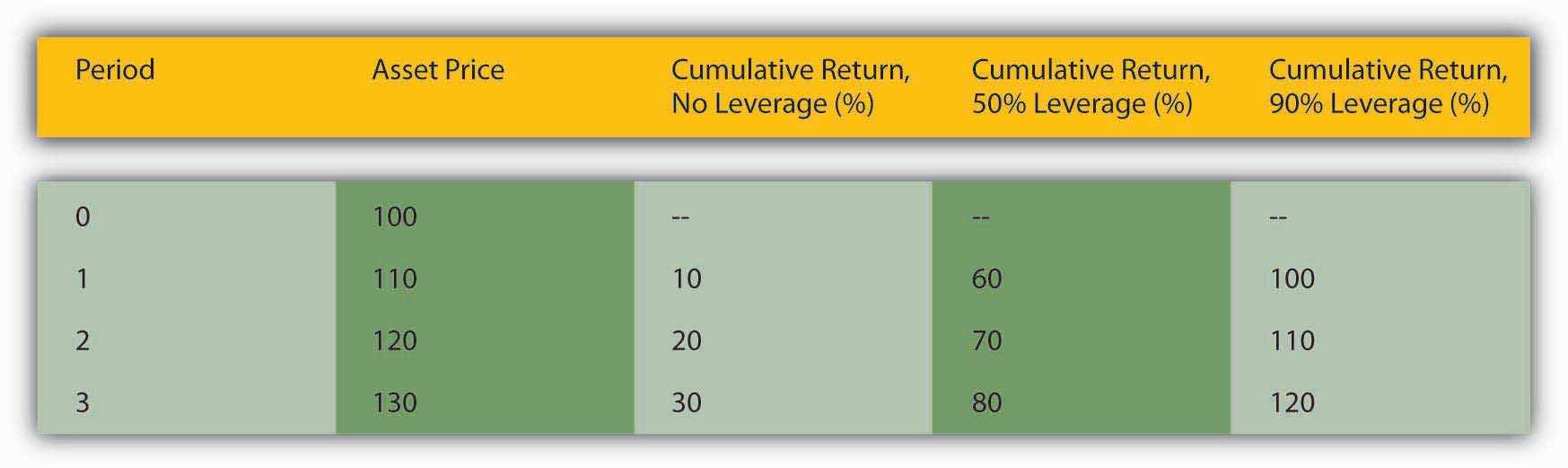
The figures were calculated using the rate of return formula: R = (C + P_t1 – P_t0)/P_t0 discussed in Chapter 4 "Interest Rates". Here, coupons are zero and hence drop out so that R = (P_t1 – P_t0)/P_t0.

In this example, returns for the unleveraged investor are great:

But the returns are not as high as the investor who borrowed half the cash, in essence paying only $50 of his own money for the $100 asset at the outset:

But even he looks like a chump compared to the investor who borrowed most of the money to finance the original purchase, putting up only $10 of his own money:

If you are thinking the most highly leveraged investor is the smart one, go back and reread the section of Chapter 2 "The Financial System" that discusses the trade-off between risk and return before continuing.