The Law of Averages

The law of averages is a lay term used to express a belief that outcomes of a random event will "even out" within a small sample. As invoked in everyday life, the "law" usually reflects bad statistics or wishful thinking rather than any mathematical principle. While there is a real theorem that a random variable will reflect its underlying probability over a very large sample (the law of large numbers), the law of averages typically assumes that unnatural short-term "balance" must occur.

The law of averages is sometimes known as "Gambler's Fallacy. " It evokes the idea that an event is "due" to happen. For example, "The roulette wheel has landed on red in three consecutive spins. The law of averages says it's due to land on black! " Of course, the wheel has no memory and its probabilities do not change according to past results. So even if the wheel has landed on red in ten consecutive spins, the probability that the next spin will be black is still 48.6% (assuming a fair European wheel with only one green zero: it would be exactly 50% if there were no green zero and the wheel were fair, and 47.4% for a fair American wheel with one green "0" and one green "00"). (In fact, if the wheel has landed on red in ten consecutive spins, that is strong evidence that the wheel is not fair - that it is biased toward red. Thus, the wise course on the eleventh spin would be to bet on red, not on black: exactly the opposite of the layman's analysis.) Similarly, there is no statistical basis for the belief that lottery numbers which haven't appeared recently are due to appear soon.

The Law of Large Numbers

Some people interchange the law of averages with the law of large numbers, but they are different. The law of averages is not a mathematical principle, whereas the law of large numbers is. In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.

The law of large numbers is important because it "guarantees" stable long-term results for the averages of random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. It is important to remember that the law of large numbers only applies (as the name indicates) when a large number of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a streak of one value will immediately be "balanced" by the others.

Another good example comes from the expected value of rolling a six-sided die. A single roll produces one of the numbers 1, 2, 3, 4, 5, or 6, each with an equal probability ($\frac{1}{6}$) of occurring. The expected value of a roll is 3.5, which comes from the following equation:

$\displaystyle \frac{1+2+3+4+5+6}{6}=3.5$

According to the law of large numbers, if a large number of six-sided dice are rolled, the average of their values (sometimes called the sample mean) is likely to be close to 3.5, with the accuracy increasing as more dice are rolled . However, in a small number of rolls, just because ten 6's are rolled in a row, it doesn't mean a 1 is more likely the next roll. Each individual outcome still has a probability of $\frac{1}{6}$.

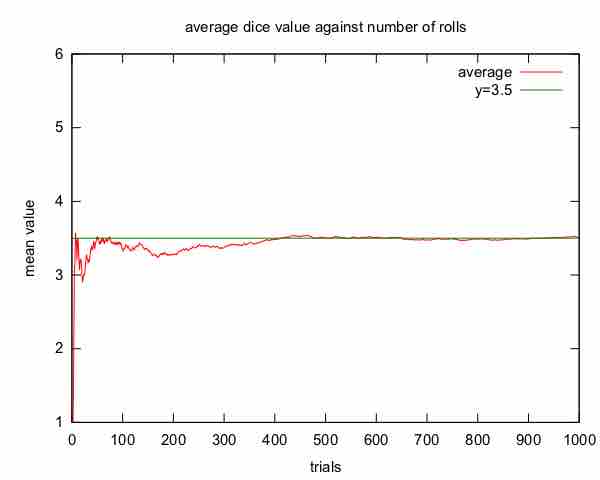
The Law of Large Numbers

This shows a graph illustrating the law of large numbers using a particular run of rolls of a single die. As the number of rolls in this run increases, the average of the values of all the results approaches 3.5. While different runs would show a different shape over a small number of throws (at the left), over a large number of rolls (to the right) they would be extremely similar.