A measure of central tendency (also referred to as measures of center or central location) is a summary measure that attempts to describe a whole set of data with a single value that represents the middle or center of its distribution. There are three main measures of central tendency: the mode, the median and the mean . Each of these measures describes a different indication of the typical skewness in the distribution.
Mean, Media and Mode
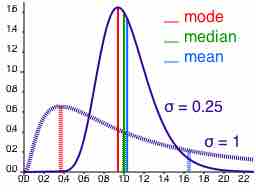
Comparison of mean, median and mode of two log-normal distributions with different skewness.
The mode is the most commonly occurring value in a distribution. Consider this dataset showing the retirement age of 11 people, in whole years:
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
The most commonly occurring value is 54, therefore the mode of this distribution is 54 years. The mode has an advantage over the median and the mean as it can be found for both numerical and categorical (non-numerical) data.
There are some limitations to using the mode. In some distributions, the mode may not reflect the center of the distribution very well. When the distribution of retirement age is ordered from lowest to highest value, it is easy to see that the center of the distribution is 57 years, but the mode is lower, at 54 years. It is also possible for there to be more than one mode for the same distribution of data, (bi-modal, or multi-modal). The presence of more than one mode can limit the ability of the mode in describing the center or typical value of the distribution because a single value to describe the center cannot be identified. In some cases, particularly where the data are continuous, the distribution may have no mode at all (i.e. if all values are different). In cases such as these, it may be better to consider using the median or mean, or group the data in to appropriate intervals, and find the modal class.