Until recently, any review of literature on multiple linear regression would tend to focus on inadequate checking of diagnostics because, for years, linear regression was used inappropriately for data that were really not suitable for it. The advent of generalized linear modelling has reduced such inappropriate use.
A key issue seldom considered in depth is that of choice of explanatory variables. There are several examples of fairly silly proxy variables in research - for example, using habitat variables to "describe" badger densities. Sometimes, if the data does not exist, it might be better to actually gather some - in the badger case, number of road kills would have been a much better measure. In a study on factors affecting unfriendliness/aggression in pet dogs, the fact that their chosen explanatory variables explained a mere 7% of the variability should have prompted the authors to consider other variables, such as the behavioral characteristics of the owners.
In addition, multicollinearity between explanatory variables should always be checked using variance inflation factors and/or matrix correlation plots . Although it may not be a problem if one is (genuinely) only interested in a predictive equation, it is crucial if one is trying to understand mechanisms. Independence of observations is another very important assumption. While it is true that non-independence can now be modeled using a random factor in a mixed effects model, it still cannot be ignored.
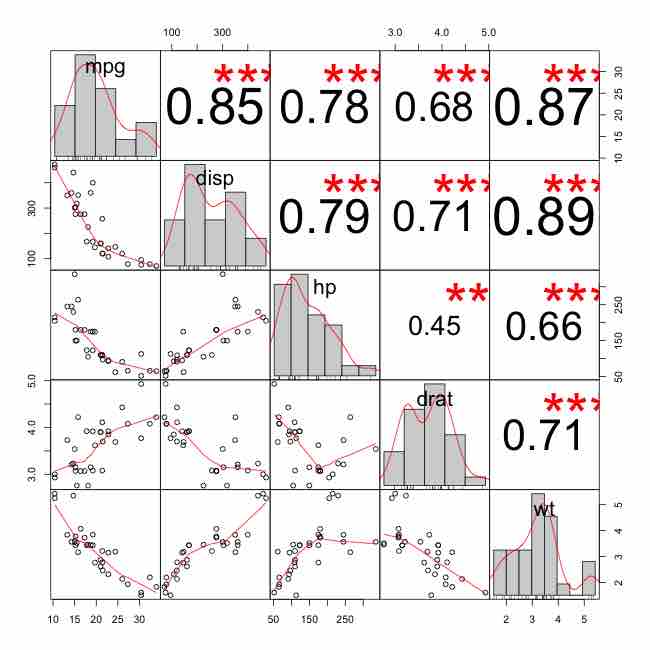
Matrix Correlation Plot
This figure shows a very nice scatterplot matrix, with histograms, kernel density overlays, absolute correlations, and significance asterisks (0.05, 0.01, 0.001).
Perhaps the most important issue to consider is that of variable selection and model simplification. Despite the fact that automated stepwise procedures for fitting multiple regression were discredited years ago, they are still widely used and continue to produce overfitted models containing various spurious variables. As with collinearity, this is less important if one is only interested in a predictive model - but even when researchers say they are only interested in prediction, we find they are usually just as interested in the relative importance of the different explanatory variables.
Quality of Extrapolation
Typically, the quality of a particular method of extrapolation is limited by the assumptions about the regression function made by the method. If the method assumes the data are smooth, then a non-smooth regression function will be poorly extrapolated.
Even for proper assumptions about the function, the extrapolation can diverge strongly from the regression function. This divergence is a specific property of extrapolation methods and is only circumvented when the functional forms assumed by the extrapolation method (inadvertently or intentionally due to additional information) accurately represent the nature of the function being extrapolated.