Overview
Imagine you are holding one end of a string, and the other end is secured and the string is pulled tight. Now, if you were to flick the string either up and down. The wave that occurs due to this motion is called a transverse wave. A transverse wave is defined as a wave where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. shows this in a diagram. In this case, the medium through which the waves propagate is the rope. The wave traveled from one end to the other, while the rope moved up and down.
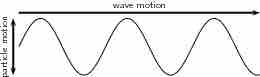
Transverse Wave
Diagram of a transverse wave. The wave motion moves perpendicular to the medium it is traveling in.
Properties of Waves
- Transverse waves have what are called peaks and troughs. The peak is the crest, or top point of the wave and the trough is the valley or bottom point of the wave.
- The amplitude is the maximum displacement of a particle from its equilibrium position.
- Wavelength, usually denoted with a lambda (λ) and measured in meters, is the distance from either one peak to the next peak, or one trough to the next trough.
- Period, usually denoted as T and measured in seconds, is the time it takes for two successive peaks, or one wavelength, to pass through a fixed point.
-
Frequency, f, is the number of wavelengths that pass through a given point in 1 second. Frequency is measured by taking the reciprocal of a period:
$\small{\rm{\textit{f}=\frac1T}}$ - Transverse waves can occur while being fixed at the end point or while being free at the end point.
Reflections of Transverse Waves
The way in which a transverse wave reflects depends on whether or not it is fixed at both ends. First we will look at waves that are fixed at both ends:
shows an image of a transverse wave that is reflected from a fixed end. When a transverse wave meets a fixed end, the wave is reflected, but inverted. This swaps the peaks with the troughs and the troughs with the peaks.

Transverse Wave With a Fixed End Point
A transverse wave that is fixed at the end point. The reflected wave is inverted.
is an image of a transverse wave on a string that meets a free end. The wave is reflected, but unlike a transverse wave with a fixed end, it is not inverted.

Transverse Wave With a Free End
When a transverse wave meets a free end, it is reflected.
Standing Waves
When either of the two scenarios of wave reflection occurs, the incident wave meets the reflected wave. These waves move past each other in opposite directions, causing interference. When these two waves have the same frequency, the product of this is called the standing waves. Standing waves appear to be standing still, hence the name. To understand how standing waves occur, we can analyze them further: When the incident wave and reflected wave first meet, both waves have an amplitude is zero. As the waves continue to move past each other, they continue to interfere with each other either constructively of destructively.
As you may remember from previous atoms, when waves are completely in phase and interfere with each other constructively, they are amplified, and when they are completely out of phase and interfere destructively they cancel out. As the waves continue to move past each other, and are reflected from the opposite end, they continue to interfere both ways, and a standing wave is produced.
Every point in the medium containing a standing wave oscillates up and down and the amplitude of the oscillations depends on the location of the point. When we observe standing waves on strings, it looks like the wave is not moving and standing still. The principle of standing waves is the basis of resonance and how many musical instruments get their sound. The points in a standing wave that appear to remain flat and do not move are called nodes. The points which reach the maximum oscillation height are called antinodes.