Working in Four Dimensions
Let us examine two observers who are moving relative to one another at a constant velocity. We shall denote them as observer A and observer A'. Observer A sets up a space-time coordinate system (t, x, y, z); similarly, A' sets up his own space-time coordinate system (t', x', y', z'). (See for an example. ) Therefore both observers live in a four-dimensional world with three space dimensions and one time dimension.
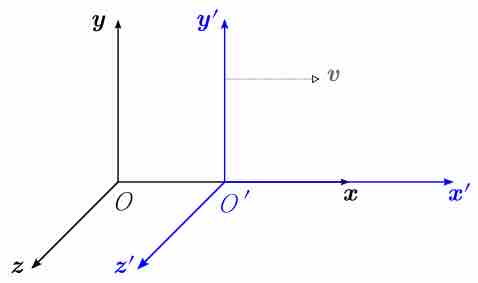
Two Coordinate Systems
Two coordinate systems in which the primed frame moves with velocity v with respect to the unprimed frame
You should not find it odd to work with four dimensions; any time you have to meet your friend somewhere you have to tell him four variables: where (three spatial coordinates) and when (one time coordinate). In other words, we have always lived in four dimensions, but so far you have probably thought of space and time as completely separate.
The Movement of Light in Four Dimensions
Back to our example: let us assume that at some point in space-time there is a beam of light that emerges. Both observers measure how far the beam has traveled at each point in time and how long it took to travel to travel that distance. That is to say, observer A measures:
where, for example,
Similarly, observer A' measures:
where we set up the system such that both observers agree on
where
This is known as the line element and is the same for all observers. (Using the principles of relativity, you can prove this for general separations, not just light rays). The set of all coordinate transformations that leave the above quantity invariant are known as Lorentz Transformations. It follows that the coordinate systems of all physical observers are related to each other by Lorentz Transformations. (The set of all Lorentz transformations form what mathematicians call a group, and the study of group theory has revolutionized physics). For the coordinate transformation in , the transformations are:
where
We define the separation between space-time points as follows:
We separate these events because they are very different. For example, for a space-like separation you can always find a coordinate transformation that reverses the time-ordering of the events (try to prove this for the example in ). This phenomenon is known as the relativity of simultaneity and may be counterintuitive.
Space-Like Space-Time Separations
Let us examine two car crashes, one in New York and one in London, such that they occur in the same time in one frame. In this situation, the space-time separation between the two events is space-like. The question of whether the events are simultaneous is relative: in some reference frames the two accidents may happen at the same time; in other frames (in a different state of motion relative to the events) the crash in London may occur first; and in still other frames the New York crash may occur first. (In practice, this does not affect us because the frames that switch the order of the events must move at unreachably high speeds. )
Time-Like and Null Space-Time Separations
Events that are time-like or null do not share this property, and therefore there is a causal ordering between time-like events. In other words, if two events are time-like separated, then they can effect each other. The reason is that if two space-time points are time-like or null separated, one can always send a light signal from one point to another.
Special Relativity
Finally, let's discuss an important result of special relativity -- that the energy
where