Physics Textbooks Boundless Physics Geometric Optics Lenses
Physics Textbooks Boundless Physics Geometric Optics
Physics Textbooks Boundless Physics
Physics Textbooks
Physics
Concept Version 9
Created by Boundless

The Lensmaker's Equation

The lensmaker's formula is used to relate the radii of curvature, the thickness, the refractive index, and the focal length of a thick lens.

Learning Objective

  • Compare idealized thin lenses with real lenses

Key Points

    • If a lens is biconvex, a beam of light travelling parallel to the lens axis and passing through the lens will be focused to a spot on the axis, at a certain distance behind the lens (i.e. the focal length). In this case, the lens is called a positive or converging lens. See.
    • If a lens is biconcave, a beam of light passing through the lens is diverged (spread); the lens is thus called a negative or diverging lens. See.
    • The focal length of a thick lens in air can be calculated from the lensmaker's equation: $P=\frac{1}{f}=(n-1)[\frac{1}{R_1}-\frac{1}{R_2}+\frac{(n-1)d}{n R_1 R_2}]$.
    • The signs of the lens' radii of curvature indicate whether the corresponding surfaces are convex or concave. The signs are reversed for the back surface of the lens: if R2 is positive the surface is concave, and if R2 is negative the surface is convex.
    • The lensmaker's equation can be greatly simplified if the lens thickness d is very small compared to R1 and R2. In this case, the thin lens approximation can then be made and the lensmaker's equation can be approximated as $P=\frac{1}{f} \approx (n-1)[\frac{1}{R_1}-\frac{1}{R_2}]$.

Terms

  • surface vertices

    The points where each surface crosses the optical axis. They are important primarily because they are the physically measurable parameters for the position of the optical elements, and so the positions of the other cardinal points must be known with respect to the vertices to describe the physical system.

  • thick lens

    Lenses whose thicknesses are not negligible (i.e., one cannot make the simple assumption that a light ray is refracted only once in the lens).

Full Text

The Lensmaker's Equation

Thick Lenses

Unlike idealized thin lenses, real lenses have a finite thickness between their two surfaces of curvature. An ideal thin lens with two surfaces of equal curvature would have zero optical power, meaning that it would neither converge nor diverge light. A lens whose thickness is not negligible is called a thick lens. In this case, we can not simply assume that a light ray is only refracted once while traveling through the lens. Instead the extent of the refraction must be dependent on the thickness of the lens.

Lenses are classified by the curvature of the two optical surfaces. A lens is biconvex (or double convex, or just convex) if both surfaces are convex. If the lens is biconvex, a beam of light travelling parallel to the lens axis and passing through the lens will be converged (or focused) to a spot on the axis, at a certain distance behind the lens (i.e. the focal length). In this case, the lens is called a positive or converging lens. See for a diagram of a positive (converging) lens.

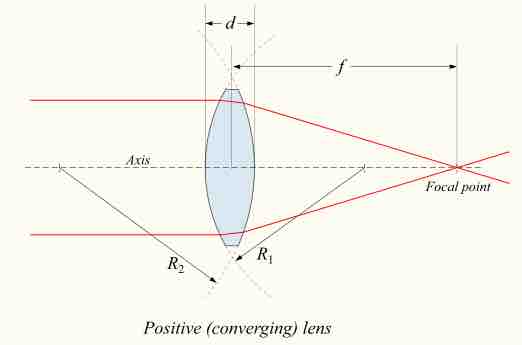
Thick Converging Lens

Diagram of a positive (converging) lens. The lensmaker's formula relates the radii of curvature, the index of refraction of the lens, the thickness of the lens, and the focal length.

If the lens is biconcave, a beam of light passing through the lens is diverged (spread); the lens is thus called a negative or diverging lens. The beam after passing through the lens appears to be emanating from a particular point on the axis in front of the lens; the distance from this point to the lens is also known as the focal length, although it is negative with respect to the focal length of a converging lens. See for a diagram of a negative (diverging) lens.

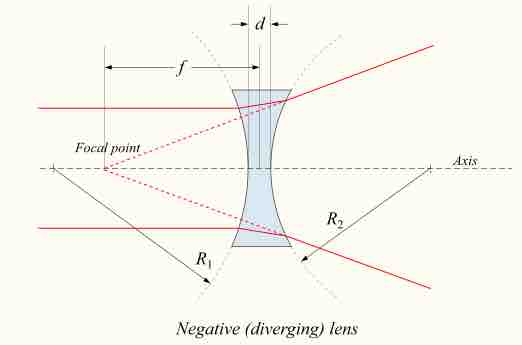
Negative Diverging Lens

Diagram of a negative (diverging) lens. The lensmaker's formula relates the radii of curvature, the index of refraction of the lens, the thickness of the lens, and the focal length.

The focal length of a thick lens in air can be calculated from the lensmaker's equation:

$P=\frac{1}{f}=(n-1)[\frac{1}{R_1}-\frac{1}{R_2}+\frac{(n-1)d}{n R_1 R_2}]$

where

  • P is the power of the lens,
  • f is the focal length of the lens,
  • n is the refractive index of the lens material,
  • R1is the radius of curvature of the lens surface closest to the light source,
  • R2 is the radius of curvature of the lens surface farthest from the light source, d and is the thickness of the lens (the distance along the lens axis between the two surface vertices).

Sign convention of Radii R1 and R2

The signs of the lens' radii of curvature indicate whether the corresponding surfaces are convex or concave. The sign convention used to represent this varies, but for our treatment if R1 is positive the first surface is convex, and if R1 is negative the surface is concave. The signs are reversed for the back surface of the lens: if R2 is positive the surface is concave, and if R2 is negative the surface is convex. If either radius is infinite, the corresponding surface is flat. With this convention the signs are determined by the shapes of the lens surfaces, and are independent of the direction in which light travels through the lens.

Thin Lens Approximation

The above equation can be greatly simplified if the lens thickness d is very small compared to R1 and R2. In this case, the thin lens approximation can then be made and the lensmaker's equation can be approximated as

$P=\frac{1}{f} \approx (n-1)[\frac{1}{R_1}-\frac{1}{R_2}]$

The focal length f is positive for converging lenses, and negative for diverging lenses. The reciprocal of the focal length, 1/f, is the optical of the lens. If the focal length is in meters, this gives the optical power in diopters (inverse meters).

Lenses have the same focal length when light travels from the back to the front as when light goes from the front to the back, although other properties of the lens, such as the aberrations are not necessarily the same in both directions.

[ edit ]
Edit this content
Prev Concept
Combinations of Lenses
Refraction Through Lenses
Next Concept