Thus far, we have looked at electric field lines pertaining to isolated point charges. But what if another charge is introduced? Each will have its own electric field, and the two fields will interact.
When modeling the electric fields of multiple charges, it's important to take into consideration the sign and magnitude of each charge. Such models are not meant to be absolute, but must be self-consistent. For example, the number field of lines should be proportional to the value of the charge that gives rise to them. This means that if charges q1 (with a +1 value) q2 (+2 charge) and q3 (+3 charge) are in the same field, one can connect 4, 8, and 12 field lines, respectively, to the charges. One could also choose to connect 3, 6, and 9 field lines, respectively, to q1, q2, and q3; what matters is that the number of lines are related to the charge values by the same proportionality constant. Field lines should always point away from positive charges and towards negative charge.
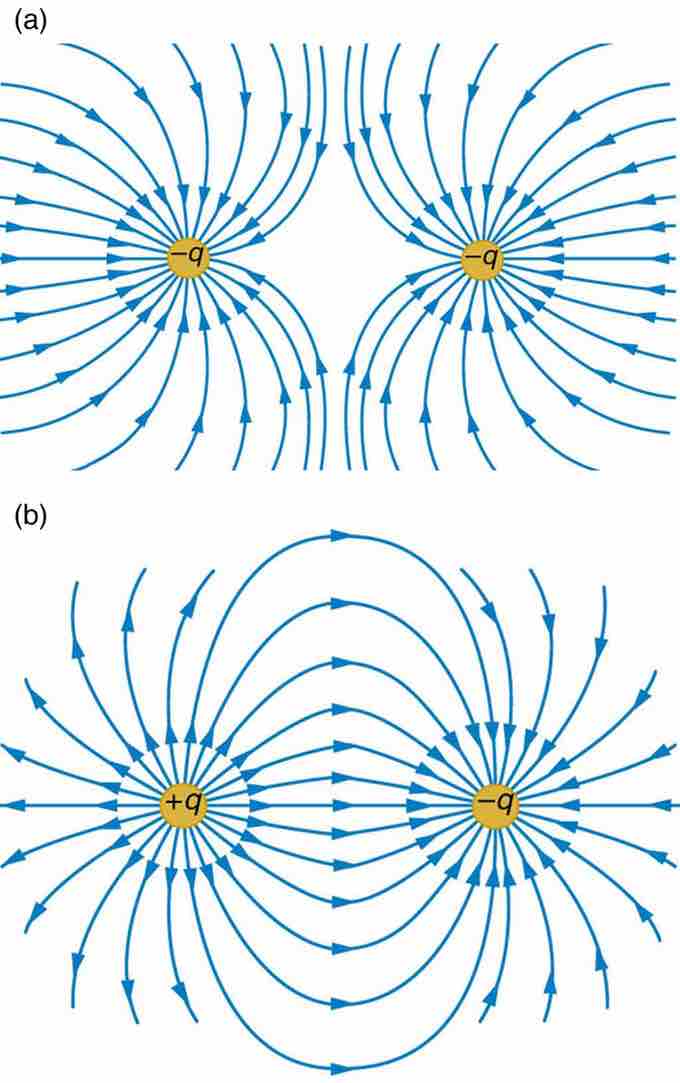
Field lines between like and unlike charges
Example a shows how the electric field is weak between like charges (the concentration of field lines is low between them). Example b, by contrast, has a strong field between the charges, as exhibited by the high concentration of field lines connecting them.
If there are opposite charges in consideration, connect one to the other with field lines. If charges are the same, do not connect them in any way.
The strength of the electric field depends proportionally upon the separation of the field lines. More field lines per unit area perpendicular to the lines means a stronger field. It should also be noted that at any point, the direction of the electric field will be tangent to the field line.
Determining net force on a test charge
As vector fields, electric fields exhibit properties typical of vectors and thus can be added to one another at any point of interest. Thus, given charges q1, q2 ,... qn, one can find their resultant force on a test charge at a certain point using vector addition: adding the component vectors in each direction and using the inverse tangent function to solve for the angle of the resultant relative to a given axis.