From Bohr's assumptions, we will now derive a number of important properties of the hydrogen atom from the classical physics. We start by noting the centripetal force causing the electron to follow a circular path is supplied by the Coulomb force. To be more general, we note that this analysis is valid for any single-electron atom. So, if a nucleus has
The spectra of hydrogen-like ions are similar to hydrogen, but shifted to higher energy by the greater attractive force between the electron and nucleus. The magnitude of the centripetal force is
This equation determines the electron's speed at any radius:
It also determines the electron's total energy at any radius:
The total energy is negative and inversely proportional to
Now, here comes the Quantum rule: As we saw in the previous module, the angular momentum
Substituting the expression in the equation for speed above gives an equation for
The allowed orbit radius at any n is then:
The smallest possible value of
Using this equation, the energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels:
Which is the Rydberg formula describing all the hydrogen spectrum and
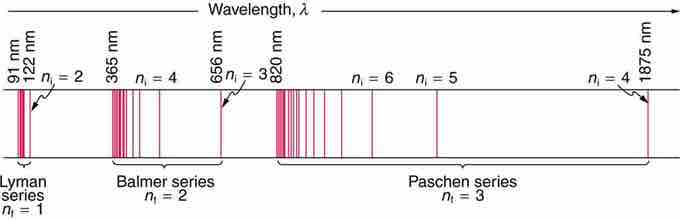
Fig 1
A schematic of the hydrogen spectrum shows several series named for those who contributed most to their determination. Part of the Balmer series is in the visible spectrum, while the Lyman series is entirely in the UV, and the Paschen series and others are in the IR. Values of nf and ni are shown for some of the lines.