The most valuable aim of capital budgeting is to rank investment proposals. To choose the most valuable investment option, several methods are commonly used:

Investment Proposal
Choosing the best investment proposal for business
Net Present Value (NPV):
NPV can be described as the "difference amount" between the sums of discounted: cash inflows and cash outflows. In the case when all future cash flows are incoming, and the only outflow of cash is the purchase price, the NPV is simply the PV of future cash flows minus the purchase price (which is its own PV). The higher the NPV, the more attractive the investment proposal. NPV is a central tool in discounted cash flow (DCF) analysis and is a standard method for using the time value of money to appraise long-term projects. Used for capital budgeting and widely used throughout economics, finance, and accounting, it measures the excess or shortfall of cash flows, in present value terms, once financing charges are met.
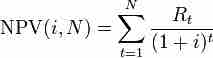
NPV formula
Each cash inflow/outflow is discounted back to its present value (PV). Then they are summed. Therefore, NPV is the sum of all terms.
In financial theory, if there is a choice between two mutually exclusive alternatives, the one yielding the higher NPV should be selected. The rules of decision making are:
- When NPV > 0, the investment would add value to the firm so the project may be accepted
- When NPV < 0, the investment would subtract value from the firm so the project should be rejected
- When NPV = 0, the investment would neither gain nor lose value for the firm. We should be indifferent in the decision whether to accept or reject the project. This project adds no monetary value. Decision should be based on other criteria (e.g., strategic positioning or other factors not explicitly included in the calculation).
An NPV calculated using variable discount rates (if they are known for the duration of the investment) better reflects the situation than one calculated from a constant discount rate for the entire investment duration.
Internal Rate of Return (IRR)
The internal rate of return on an investment or project is the "annualized effective compounded return rate" or "rate of return" that makes the net present value (NPV as NET*1/(1+IRR)^year) of all cash flows (both positive and negative) from a particular investment equal to zero.
IRR calculations are commonly used to evaluate the desirability of investments or projects. The higher a project's IRR, the more desirable it is to undertake the project. Assuming all projects require the same amount of up-front investment, the project with the highest IRR would be considered the best and undertaken first.
Profitability Index (PI)
It is a useful tool for ranking projects, because it allows you to quantify the amount of value created per unit of investment. The ratio is calculated as follows:
Profitability index = PV of future cash flows / Initial investment
As the value of the profitability index increases, so does the financial attractiveness of the proposed project. Rules for selection or rejection of a project:
- If PI > 1 then accept the project
- If PI < 1 then reject the project
Payback Period
Payback period intuitively measures how long something takes to "pay for itself. " All else being equal, shorter payback periods are preferable to longer payback periods. Payback period is widely used because of its ease of use despite the recognized limitations: The time value of money is not taken into account.
Accounting Rate of Return (ARR)
The ratio does not take into account the concept of time value of money. ARR calculates the return, generated from net income of the proposed capital investment. The ARR is a percentage return. Say, if ARR = 7%, then it means that the project is expected to earn seven cents out of each dollar invested. If the ARR is equal to or greater than the required rate of return, the project is acceptable. If it is less than the desired rate, it should be rejected. When comparing investments, the higher the ARR, the more attractive the investment. Basic formulae:
ARR = Average profit / Average investment
Where: Average investment = (Book value at beginning of year 1 + Book value at end of user life) / 2