Arbitrage Pricing Theory

The Arbitrage Pricing Theory (APT) is a linear relationship between systemic factors and the return of an asset.

Learning Objective

Describe the strengths and weaknesses of the Arbitrage Pricing Theory.

Key Points

APT was proposed by Stephen Ross in 1976 as a way to price assets.
APT differs from CAPM by allowing for multiple explanatory factors.
APT is not 100% accurate, but s still used as the basis for many of the commercial risk systems employed by asset managers.

Full Text

Arbitrage Pricing Theory (APT) is a model for asset pricing that was proposed by Stephen Ross in 1976. It is a generalized linear function for determining the price of an asset.

The expected return of asset j under APT can be expressed in the following form:

$r_j = a_j + b_{j1}F_1 + b_{j2}F_2 + \cdots + b_{jn}F_n + \epsilon_j$

where r is the return, a is a constant, each F is a systematic factor, each b is the sensitivity of the asset to the factor (factor loading), and epsilon is an error term that captures idiosyncratic random shocks (with a mean value of zero). One of the most important aspects of APT is that, like CAPM, the relationship between each factor and the return is linear. Unlike CAPM, however, APT allows for there to be multiple factors that explain the return .

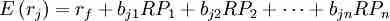
Expected Returns Under APT

APT can also be expressed in terms of expected returns where RP is the risk premium of the factor, and rf is the risk-free rate.

Implicit in APT are two notable assumptions:

There is perfect competition in the market
The total number of factors does not exceed the total number of assets (this is due to a mathematical constraint that is beyond the scope of this text)

Naturally, this means that there are limits to how accurate APT is in the real world, but APT is still used as the basis for many of the commercial risk systems employed by asset managers.

If an asset is either over- or under-priced, then there is an arbitrage opportunity. Market actors will take advantage of this opportunity, and through buying or selling the asset, push the price of the asset back to its true value.

[ edit ]