Free Energy Changes for Nonstandard States

The apparent similarity of the terms $\Delta G$, $\Delta G^{\circ}$ and $\Delta G_f^{\circ}$ makes it easy to overlook the distinctions between them; the similarity is a major source of confusion. The most important thing to remember is that the terms $\Delta G^{\circ}$and $\Delta G_f^{\circ}$ refer to single, specific chemical changes in which all components (reactants and products) are in their standard states.

Plotting

The distinction is nicely illustrated in this diagram , in which $\Delta G$ is plotted on a vertical axis for two hypothetical reactions having opposite signs of $\Delta G^{\circ}$. The horizontal axis schematically expresses the relative concentrations of reactants and products at any point of the process. Note that the origin corresponds to the composition at which half of the reactants have been converted into products.

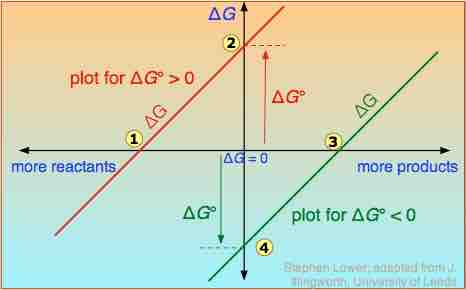
ΔG vs. G°

ΔG is plotted on a vertical axis for two hypothetical reactions having opposite signs of ΔG°.

Take careful note of the following:

• The red line on the left plots the values of $\Delta G$ for the $\Delta G^{\circ}$ > 0 reaction. Notice that there are an infinite number of these values, depending on the progress of the reaction. In contrast, there is only a single value (point 2) of $\Delta G^{\circ}$, corresponding to the composition at which $\Delta G$ = 0 (point 1).
• At this point, some products have been formed, but the composition is still dominated by reactants.
• If the reaction begins at a composition to the left of point 1 on the diagram, $\Delta G$ will be negative and the composition will move to the right. Similarly, if the reaction begins with a composition to the right of point 1 on the diagram, $\Delta G$ will be positive and the composition will move to the left.
• The plot on the right is for the $\Delta G^{\circ}$ < 0 reaction, for which $\Delta G^{\circ}$is shown at point 4 on the diagram. At its equilibrium point (point 3), there are more products than reactants. If the reaction starts at a composition to the right of point 3 on the diagram, the composition will tend to move to the left. If the initial composition is to the left of point 3 on diagram, the reaction will tend to proceed to the right.
• What would happen if $\Delta G^{\circ}$ were 0? The equilibrium point of such a reaction would be at the origin, corresponding to half the reactants being converted to products.

The important principle to understand is that a negative $\Delta G^{\circ}$ does not mean that the reactants will be completely transformed into products. By the same token, a positive $\Delta G^{\circ}$ does not mean that no products are formed at all.

Possible Values

In contrast, the composition of a chemical reaction system undergoes continual change until the equilibrium state is reached. Therefore, a single reaction can have an infinite number of $\Delta G$ values, reflecting the infinite possible compositions between the extremes of pure reactants and pure products.

In the example of a reaction $A \rightarrow B$, depicted in the following diagram, the standard free energy of the products (point 2) is smaller than that of the reactants (point 1), so the reaction will take place spontaneously. This does not mean that each mole of pure A will be converted into one mole of pure B.

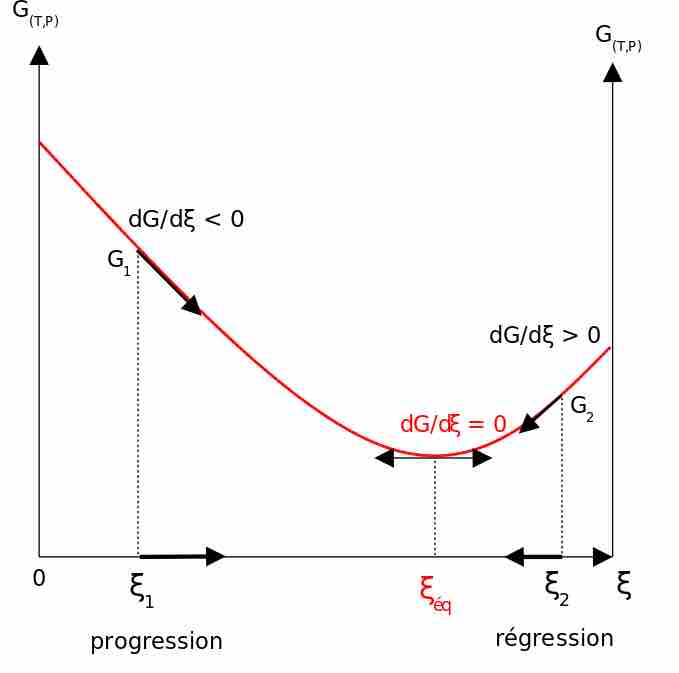
Nonstandard state free energy change

Graph of $G(T,p) = f(\xi)$. A single reaction can have an infinite number of $\Delta G$ values.

The physical meaning of $\Delta G$ is that it tells us how far the free energy of the system has changed from G° of the pure reactants (point 1). As the reaction proceeds to the right, the composition changes, and $\Delta G$ begins to fall. When the composition reaches point 3, $\Delta G$ reaches its minimum value, and further reaction would cause it to rise. But because free energy can only decrease but never increase, this does not happen. The composition of the system remains permanently at its equilibrium value.