Properties of Supercritical Fluids
A supercritical fluid is any substance at a temperature and pressure above its critical point, where distinct liquid and gas phases do not exist. This can be rationalized by thinking that at high enough temperatures (above the critical temperature) the kinetic energy of the molecules is high enough to overcome any intermolecular forces that would condense the sample into the liquid phase. On the other hand, high enough pressures (above the critical pressure) would not allow a sample to stay in the pure gaseous state. Therefore, a balance between these two tendencies is achieved and the substance exists in a state between a gas and a liquid.
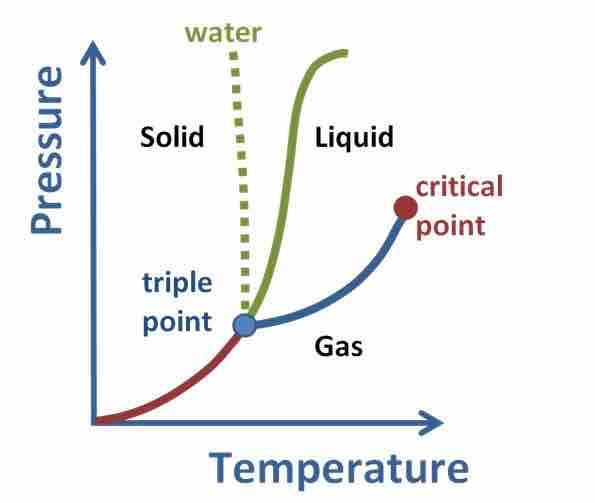
Phase Diagram for a Substance
The figure highlights the critical point, above which (in either temperature or pressure) the substance does not exist in either the liquid or gas phase. Under those conditions it is called a "supercritical fluid," and has properties between those of a liquid and a gas.
It can effuse through solids (like a gas), and dissolve materials (like a liquid). In addition, close to the critical point, small changes in pressure or temperature result in large changes in density, allowing many properties of a supercritical fluid to be "fine-tuned. " Supercritical fluids are suitable as a substitute for organic solvents in a range of industrial and laboratory processes. Carbon dioxide and water are the most commonly used supercritical fluids, as they are used for decaffeination and power generation, respectively.
In general terms, supercritical fluids have properties between those of a gas and a liquid. The critical properties of some substances used as solvents and as supercritical fluids are shown in Table 1. Table 2 shows density, diffusivity, and viscosity for typical liquids, gases, and supercritical fluids.
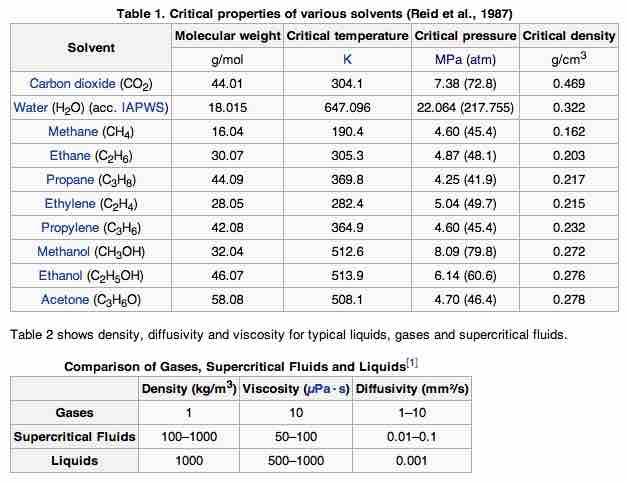
Critical Properties of Various Solvents
Supercritical fluids have properties between those of a gas and a liquid.
In addition, there is no surface tension in a supercritical fluid, as there is no liquid to gas phase boundary. By changing the pressure and temperature of the fluid, the properties can be "tuned" to be more liquid- or gas-like. One of the most important properties of supercritical fluids is their ability to act as solvents. Solubility in a supercritical fluid tends to increase with the density of the fluid (at constant temperature). Since density increases with pressure, solubility tends to increase with pressure.
The relationship with temperature is a little more complicated. At constant density, solubility will increase with temperature. However, close to the critical point, the density can drop sharply with a slight increase in temperature. Therefore, close to the critical temperature, solubility often drops with increasing temperature, then rises again.
All supercritical fluids are completely miscible with each other; therefore a single phase for a mixture can be guaranteed if the critical point is exceeded. The critical point of a binary mixture can be estimated as the arithmetic mean of the critical temperatures and pressures of the two components,
Tc(mix) = (mole fraction of A) x Tc(A) + (mole fraction of B) x Tc(B)
For greater accuracy, the critical point can be calculated using equations of state, such as the Peng Robinson or group contribution methods. Other properties, such as density, can also be calculated using equations of state.
Case Study: Carbon Dioxide
In the pressure-temperature phase diagram of CO2, the boiling separates the gas and liquid region and ends in the critical point, where the liquid and gas phases disappear to become a single supercritical phase. At well below the critical temperature, (e.g., 280 K), as the pressure increases, the gas compresses and eventually (at just over 40 bar) condenses into a much denser liquid, resulting in the discontinuity in the line (vertical dotted line). The system consists of 2 phases in equilibrium, a dense liquid and a low density gas.
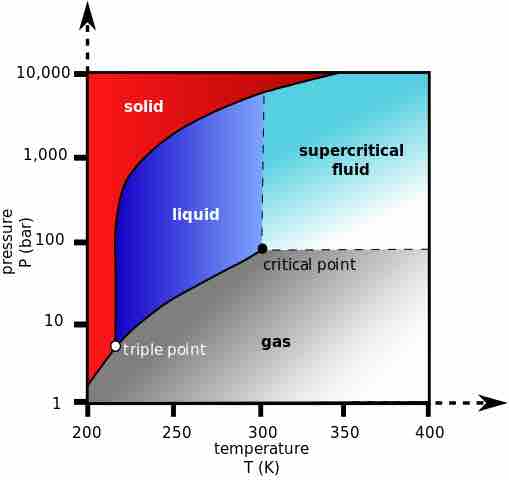
Phase Diagram for Carbon Dioxide
This diagram indicates the supercritical fluid region of CO2.
As the critical temperature is approached (300 K), the density of the gas at equilibrium becomes denser, and that of the liquid becomes lower. At the critical point, (304.1 K and 7.38 MPa) there is no difference in density, and the two phases become one fluid phase. Thus, above the critical temperature a gas cannot be liquified by pressure. At slightly above the critical temperature (310 K), in the vicinity of the critical pressure, the line is almost vertical. A small increase in pressure causes a large increase in the density of the supercritical phase. Many other physical properties also show large gradients with pressure near the critical point, such as viscosity, the relative permittivity, and the solvent strength, which are all closely related to the density.