Integration By Parts

Introduction

In calculus, integration by parts is a theorem that relates the integral of a product of functions to the integral of their derivative and anti-derivative. It is frequently used to find the anti-derivative of a product of functions into an ideally simpler anti-derivative. The rule can be derived in one line by simply integrating the product rule of differentiation.

Theorem of integration by parts

Let's take the functions $u = u(x)$ and $v = v(x)$. When taking their derivatives, we are left with $du = u '(x)$ and $dxdv = v'(x) dx$. Now, let's take a look at the principle of integration by parts:

$\displaystyle{\int u(x) v'(x) \, dx = u(x) v(x) - \int u'(x) v(x) \ dx}$

or, more compactly,

$\displaystyle{\int u \, dv=uv-\int v \, du}$

Proof

Suppose $u(x)$ and $v(x)$ are two continuously differentiable functions. The product rule states: 

$\displaystyle{\frac{d}{dx}\left(u(x)v(x)\right) = u(x) \frac{d}{dx}\left(v(x)\right) + \frac{d}{dx}\left(u(x)\right) v(x)}$

Integrating both sides with respect to $x$, over an interval $a \leq x \leq b$,

$\displaystyle{\int_a^b \frac{d}{dx}\left(u(x)v(x)\right)\,dx = \int_a^b u'(x)v(x)\,dx + \int_a^b u(x)v'(x)\,dx}$ 

then applying the fundamental theorem of calculus,

$\displaystyle{\int_a^b \frac{d}{dx}\left(u(x)v(x)\right)\,dx = \left[u(x)v(x)\right]_a^b}$

 gives the formula for "integration by parts":

$\displaystyle{\left[u(x)v(x)\right]_a^b = \int_a^b u'(x)v(x)\,dx + \int_a^b u(x)v'(x)\,dx}$.

Visulization

Let's define a parametric curve by $(x, y) = (f(t), g(t))$.

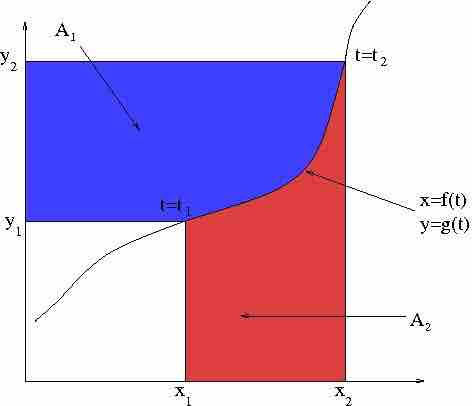
Integration By Parts

Integration by parts may be thought of as deriving the area of the blue region from the total area and that of the red region. The area of the blue region is $A_1=\int_{y_1}^{y_2}x(y)dy$. Similarly, the area of the red region is $A_2=\int_{x_1}^{x_2}y(x)dx$. The total area, $A_1+A_2$_, is equal to the area of the bigger rectangle, $x_2y_2$, minus the area of the smaller one, $x_1y_1$: $\int_{y_1}^{y_2}x(y)dy+\int_{x_1}^{x_2}y(x)dx=\biggl.x_iy_i\biggl|_{i=1}^{i=2}$. Assuming the curve is smooth within a neighborhood, this generalizes to indefinite integrals $\int xdy + \int y dx = xy$, which can be rearranged to the form of the theorem: $\int xdy = xy - \int y dx$.

Example

In order to calculate $I=\int x\cos (x) \,dx$, let:

$u = x \\ \therefore du = dx$

and

$dv = \cos(x)\,dx \\ \therefore v = \int\cos(x)\,dx = \sin x$

then:

$\begin{aligned} \int x\cos (x) \,dx & = \int u \, dv \\ & = uv - \int v \, du \\ & = x\sin (x) - \int \sin (x) \,dx \\ & = x\sin (x) + \cos (x) + C \end{aligned}$