Integration is an important concept in mathematics and—together with its inverse, differentiation—is one of the two main operations in calculus. Given a function
Definite Integral
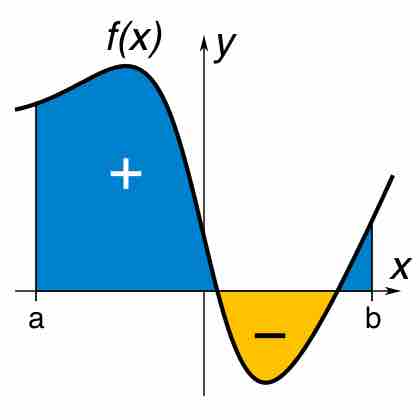
A definite integral of a function can be represented as the signed area of the region bounded by its graph.
More rigorously, once an anti-derivative
If
Integration proceeds by adding up an infinite number of infinitely small areas. This sum can be computed by using the anti-derivative.
Properties
Linearity
The integral of a linear combination is the linear combination of the integrals.
Inequalities
If
Additivity
If
Reversing Limits of Integration
If
Integration by Substitution
By reversing the chain rule, we obtain the technique called integration by substitution. Given two functions
or written in terms of the "dummy variable"
If we are going to use integration by substitution to calculate a definite integral, we must change the upper and lower bounds of integration accordingly.