The natural logarithm, generally written as
The derivative of the natural logarithm is given by:
This leads to the Taylor series for
for
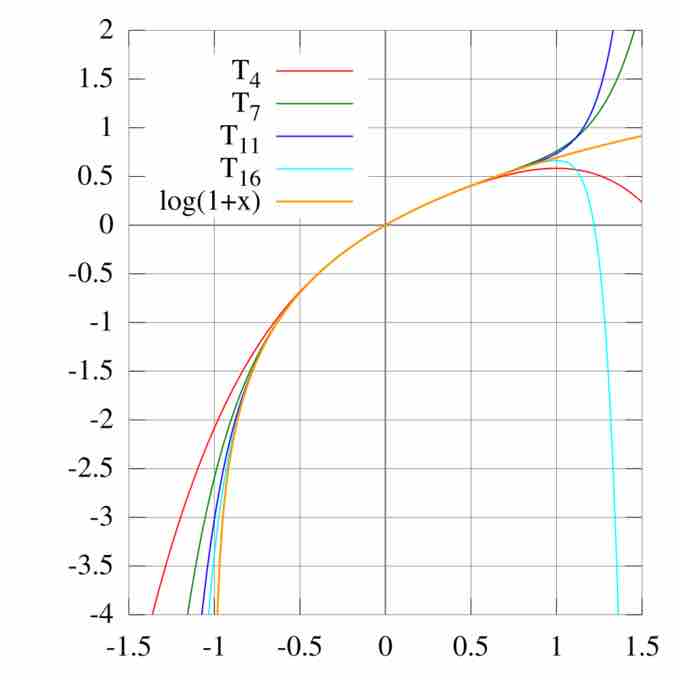
Taylor Series Approximations for $\ln(1+x)$
The Taylor polynomials for
Substituting
for
By using Euler transform, we reach the following equation, which is valid for any
The natural logarithm allows simple integration of functions of the form
In other words:
and
Here is an example in the case of
Letting
where
The natural logarithm can be integrated using integration by parts: