The Natural Exponential Function: Differentiation and Integration

Here we consider differentiation of natural exponential functions. 

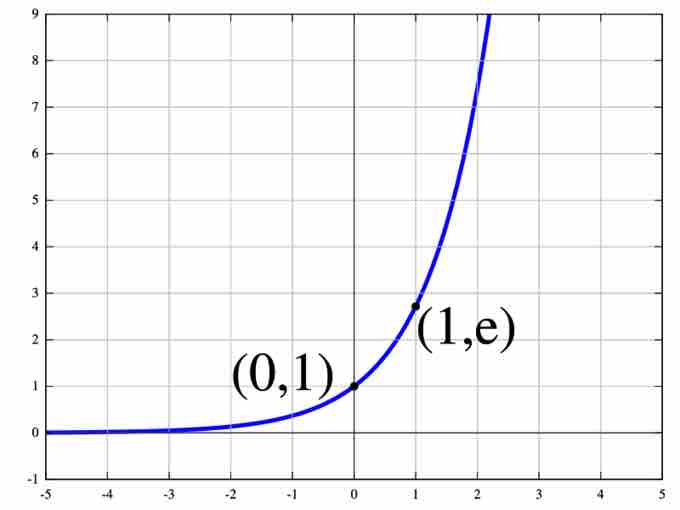
Exponential Function

The natural exponential function $y = e^x$.

First, we determine the derivative of $e^{x}$ using the definition of the derivative:

$\dfrac{d}{dx}e^{x} =\lim_{h \to 0}\dfrac{e^{x + h} - e^{x}}{h}$

Then we apply some basic algebra with powers:

$\dfrac{d}{dx}e^{x} =\lim_{h \to 0}\dfrac{e^{x}e^{h} - e^{x}}{h}$

Since $e^{x}$ does not depend on $h$, it is constant as $h$ goes to $0$. Thus, we can use the limit rules to move it to the outside, leaving us with 

$\dfrac{d}{dx}e^{x} =e^{x}\lim_{h \to 0}\dfrac{e^{h} - 1}{h}$

The limit can then be calculated using L'Hôpital's rule: 

$\lim_{h \to 0}\dfrac{e^{h} - 1}{h} = 1$

Now we have proven the following rule: 

$\dfrac{d}{dx}e^{x} =e^{x}$

Now that we have derived a specific case, let us extend things to the general case of exponential function. Assuming that $a$ is a positive real constant, we wish to calculate the following: 

$\dfrac{d}{dx}a^{x}$

Since we have already determined the derivative of $e^{x}$, we will attempt to rewrite $a^{x}$ in that form. Using that $e^{\ln(c)} = c$ and that $\ln(ab) = b \cdot \ln(a)$, we find that: 

$a^{x} = e^{x\cdot \ln(a)}$

Now, we simply apply the chain rule: 

$\dfrac{d}{dx}e^{x\cdot \ln(a)} = \dfrac{d}{dx}\left(x\cdot \ln(a)\right)e^{x\cdot \ln(a)} = \ln(a)a^{x}$

Derivative of the exponential function: 

$\dfrac{d}{dx}a^x = \ln(a)a^{x}$

Here we consider integration of natural exponential function. Note that the exponential function $y = e^{x}$ is defined as the inverse of $\ln(x)$. Therefore $\ln(e^x) = x$ and $e^{\ln x} = x$. 

Let's consider the example of $\int e^{x}dx$. Since $e^{x} = (e^{x})'$ we can integrate both sides to get:

$\displaystyle{\int e^{x}dx = e^{x} + C}$