Predator-Prey Systems

The predator–prey equations are a pair of first-order, non-linear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one a predator and one its prey.

They evolve in time according to the pair of equations:

$\displaystyle{\frac{dx}{dt}= \alpha x - \beta xy}$

$\displaystyle{\frac{dy}{dt}= \delta xy - \gamma y}$

where $x$ is the number of prey (for example, rabbits); $y$ is the number of some predator (for example, foxes); and $\frac{dx}{dt}$ and $\frac{dy}{dt}$ represent the growth rates of the two populations over time; $t$ represents time; and $\alpha$, $\beta$, $\gamma$, and $\delta$ are parameters describing the interaction of the two species.

The model makes a number of assumptions about the environment and evolution of the predator and prey populations:

• The prey population finds ample food at all times.
• The food supply of the predator population depends entirely on the prey populations.
• The rate of change of population is proportional to its size.
• During the process, the environment does not change in favor of one species and the genetic adaptation is sufficiently slow.
• As differential equations are used, the solution is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.

The prey are assumed to have an unlimited food supply, and to reproduce exponentially unless subject to predation; this exponential growth is represented in the equation above by the term $\alpha x$. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet; this is represented above by $\beta xy$. If either $x$ or $y$ is zero, then there can be no predation. With these two terms, the equation above can be interpreted as follows: the change in the prey's number is given by its own growth minus the rate at which it is preyed upon.

In the predator equation, $\delta xy$ represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). $\gamma y$ represents the loss rate of the predators due to either natural death or emigration; it leads to an exponential decay in the absence of prey. Hence, the equation expresses the change in the predator population as growth fueled by the food supply, minus natural death.

The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions. They can only be solved numerically. However, a linearization of the equations yields a solution similar to simple harmonic motion with the population of predators following that of prey by 90 degrees.

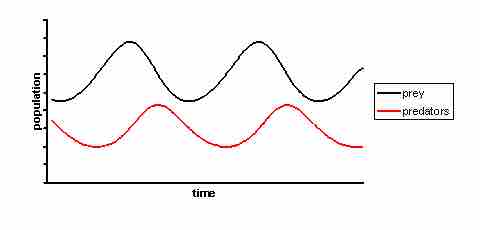
Solution to the equation

The solutions to the equations are periodic. The predator population follows the prey population.