Integration is an important concept in mathematics and—together with its inverse, differentiation—is one of the two main operations in calculus. Given a function
Definite Integral
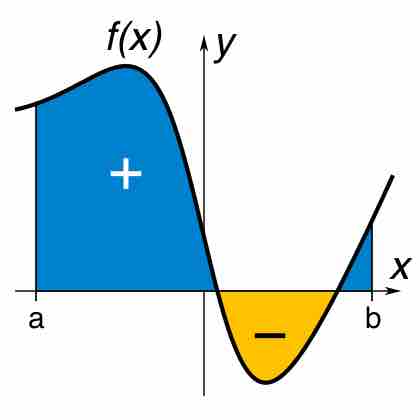
A definite integral of a function can be represented as the signed area of the region bounded by its graph.
The principles of integration were formulated independently by Isaac Newton and Gottfried Leibniz in the late 17th century. Through the fundamental theorem of calculus, which they independently developed, integration is connected with differentiation: if
Definite integrals appear in many practical situations. If a swimming pool is rectangular with a flat bottom, then from its length, width, and depth we can easily determine the volume of water it can contain (to fill it), the area of its surface (to cover it), and the length of its edge (to rope it). But if it is oval with a rounded bottom, all of these quantities call for integrals. Practical approximations may suffice for such trivial examples, but precision engineering (of any discipline) requires exact and rigorous values for these elements.
For example, consider the curve
We ask, "What is the area under the function
As a first approximation, look at the unit square given by the sides
Notice that we are taking a finite sum of many function values of
As for the actual calculation of integrals, the fundamental theorem of calculus, due to Newton and Leibniz, is the fundamental link between the operations of differentiating and integrating. Applied to the square root curve,
and simply take