Three-Dimensional Coordinate Systems

The three-dimensional coordinate system expresses a point in space with three parameters, often length, width and depth ($x$, $y$, and $z$).

Learning Objective

Identify the number of parameters necessary to express a point in the three-dimensional coordinate system

Key Points

There are many types of coordinate systems, including Cartesian, spherical, and cylindrical coordinates.
In the Cartesian system, all three of the parameters are represented as the quantitative distance from the reference plane.
In order to convert from Cartesian to spherical, you need to convert each parameter separately, as follows: $r = \sqrt{x^2+y^2+z^2}\\ \theta=\arccos (\frac{z}{r})\\ \varphi =\arctan (\frac{y}{x})$.

Terms

coordinate system
a method of representing points in a space of given dimensions by coordinates from an origin
origin
the point at which the axes of a coordinate system intersect

Full Text

The Three Dimensional Coordinate System

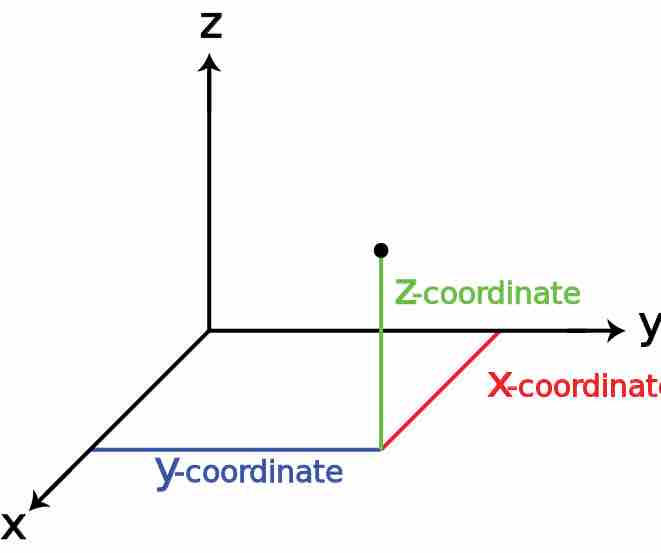
A three dimensional space has three geometric parameters: $x$, $y$, and $z$. These are often referred to as length, width and depth. Each parameter is perpendicular to the other two, and cannot lie in the same plane. shows a Cartesian coordinate system that uses the parameters $x$, $y$, and $z$.

Three-Dimensional Space

This is a three dimensional space represented by a Cartesian coordinate system.

Cartesian Geometry

Also known as analytical geometry, this system is used to describe every point in three dimensional space in three parameters, each perpendicular to the other two at the origin. Each parameter is labeled relative to its axis with a quantitative representation of its distance from its plane of reference, which is determined by the other two parameter axes.

Other Coordinate Systems

Cylindrical Coordinates ($\rho, \varphi, z$)

The cylindrical system uses two linear parameters and one radial parameter:

$\rho$: the radial distance from the point to $z$
$\varphi$: the angle between the reference direction and the point
$z$: the distance from the reference plane to the point

Cylindrical Coordinate System

The cylindrical coordinate system is like a mix between the spherical and Cartesian system, incorporating linear and radial parameters.

Spherical Coordinates ($r$, $\theta$, $\varphi$)

The spherical system is used commonly in mathematics and physics:

$r$: the radial distance from the origin to the point
$\theta$: the angle between the zenith direction and directional vector of $r$
$\varphi$: the angle from the reference direction to the orthogonal plane projected by the directional vector of $r$

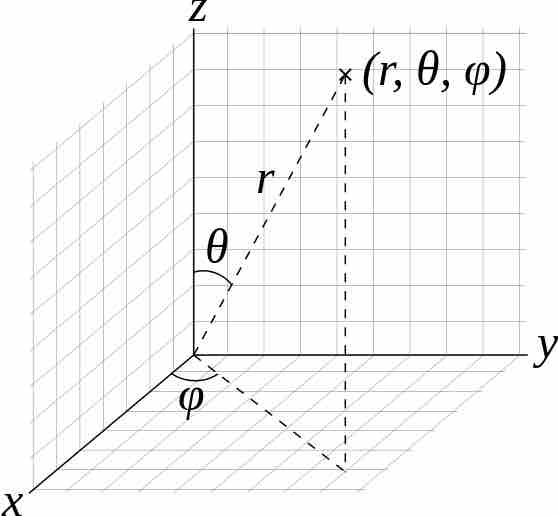
Spherical Coordinate System

The spherical system is used commonly in mathematics and physics and has variables of $r$, $\theta$, and $\varphi$.

Cartesian to Spherical

Often, you will need to be able to convert from spherical to Cartesian, or the other way around. The following equations will allow you to do just that:

$\displaystyle{r = \sqrt{x^2+y^2+z^2}}$

$\displaystyle{\theta=\arccos \left(\frac{z}{r}\right)}$

$\displaystyle{\varphi =\arctan \left(\frac{y}{x}\right)}$

[ edit ]

Prev Concept

Convergence of Series with Positive Terms

Vectors in the Plane

Next Concept