Partial Derivatives

A partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f with respect to the variable x is variously denoted by $f^\prime_x,\ f_{,x},\ \partial_x f, \text{ or } \frac{\partial f}{\partial x}$.

Suppose that f is a function of more than one variable. For instance, $z = f(x, y) = x^2 + xy + y^2$. The graph of this function defines a surface in Euclidean space . To every point on this surface, there is an infinite number of tangent lines. Partial differentiation is the act of choosing one of these lines and finding its slope. Usually, the lines of most interest are those which are parallel to the $xz$-plane and those which are parallel to the $yz$-plane (which result from holding either $y$ or $x$ constant, respectively).

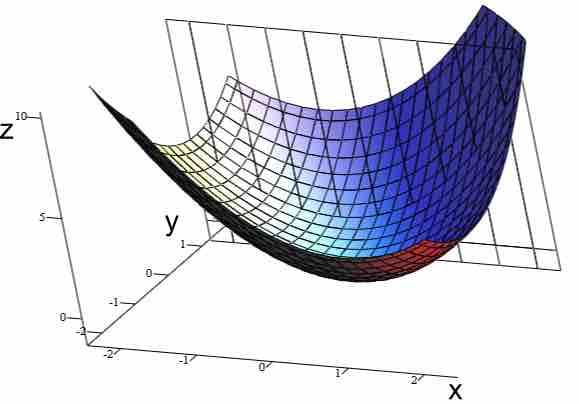
Graph of $z = x^2 + xy + y^2$

For the partial derivative at $(1, 1, 3)$ that leaves $y$ constant, the corresponding tangent line is parallel to the $xz$-plane.

To find the slope of the line tangent to the function at $P(1, 1, 3)$ that is parallel to the $xz$-plane, the $y$ variable is treated as constant. By finding the derivative of the equation while assuming that $y$ is a constant, the slope of $f$ at the point $(x, y, z)$ is found to be: 

$\displaystyle{\frac{\partial z}{\partial x} = 2x+y}$

So at $(1, 1, 3)$, by substitution, the slope is $3$. Therefore,

$\displaystyle{\frac{\partial z}{\partial x} = 3}$ 

at the point $(1, 1, 3)$. That is to say, the partial derivative of $z$ with respect to $x$ at $(1, 1, 3)$ is $3$.

Graph of $z = x^2 + xy + y^2$ at $y=1$

A slice of the graph at $y=1$.

Formal Definition

Like ordinary derivatives, the partial derivative is defined as a limit. Let $U$ be an open subset of $R^n$ and $f:U \rightarrow R$ a function. The partial derivative of $f$ at the point $a = (a_1, \cdots, a_n) \in U$ with respect to the $i$th variable  is defined as:

$\displaystyle{\frac{ \partial }{\partial a_i }f(\mathbf{a}) = \lim_{h \rightarrow 0}{ f(a_1, \cdots , a_{i-1}, a_i+h, a_{i+1}, \cdots ,a_n) - f(a_1, \cdots, a_i, \cdots ,a_n) \over h }}$