Center of Mass and Inertia

Multiple integrals are used in many applications in physics and engineering. In this atom, we will see how center of mass can be calculated using multiple integrals.

The center of mass is the unique point at the center of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero. In the case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the physical body, as is sometimes the case for hollow or open-shaped objects, such as a horseshoe. In the case of a distribution of separate bodies, such as the planets of the Solar System, the center of mass may not correspond to the position of any individual member of the system.

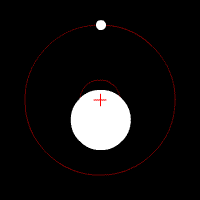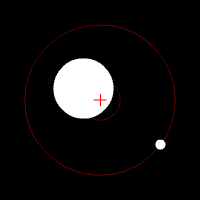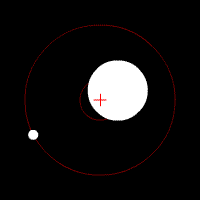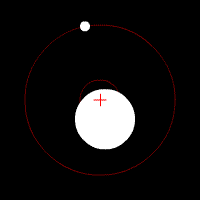
Center of Mass

Two bodies orbiting around the center of mass inside one body

A System of Particles

In the case of a system of particles $P_i, i = 1, \cdots , n$, each with mass $m_i$ that are located in space with coordinates $\mathbf{r}_i, i = 1, \cdots , n$, the coordinates $\mathbf{R}$ of the center of mass satisfy the condition:

 $\displaystyle{\sum_{i=1}^n m_i(\mathbf{r}_i - \mathbf{R}) = 0}$

Solve this equation for $\mathbf{R}$ to obtain the formula:

 $\displaystyle{\mathbf{R} = \frac{1}{M} \sum_{i=1}^n m_i \mathbf{r}_i}$

where $M$ is the sum of the masses of all of the particles.

A Continuous Volume

If the mass distribution is continuous with the density $\rho (r)$ within a volume $V$, then the integral of the weighted position coordinates of the points in this volume relative to the center of mass $\mathbf{R}$ is zero; that is:

 $\displaystyle{\int_V \rho(\mathbf{r})(\mathbf{r}-\mathbf{R})dV = 0}$

Solve this equation for the coordinates $\mathbf{R}$ to obtain:

$\displaystyle{\mathbf R = \frac 1M \int_V\rho(\mathbf{r}) \mathbf{r} dV}$

where $M$ is the total mass in the volume. The integral is over the three dimensional volume, so it is a triple integral.