The discriminant of a quadratic function is a function of its coefficients that reveals information about its roots. A root is the value of the
The discriminant for quadratic functions is:
Where
The Discriminant and the Quadratic Formula
Recall the quadratic formula:
where
The discriminant
Positive Discriminant
If
Because adding and subtracting a positive number will result in different values, a positive discriminant results in two distinct solutions, and two distinct roots of the quadratic function.
Zero Discriminant
If
Since adding zero and subtracting zero in the quadratic equation lead to the same outcome, there is only one distinct root of the quadratic function.
Negative Discriminant
If
This means the square root itself is an imaginary number, so the roots of the quadratic function are distinct and not real.
Example
Consider the quadratic function:
Using
Because Δ is greater than zero, the function has two distinct, real roots. Checking graphically, we can confirm this is true; the zeros of the function can be found at
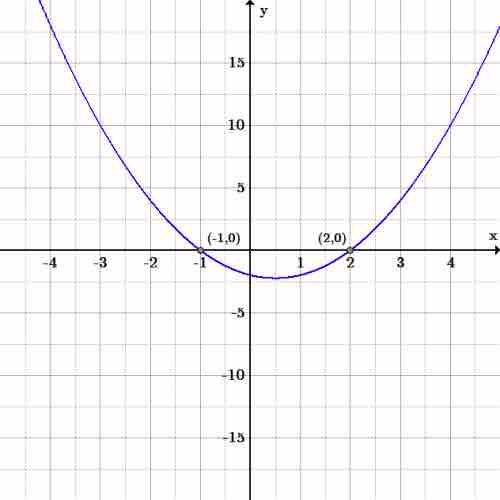
Example
Graph of a polynomial with the quadratic function