Linear Inequalities

When two linear expressions are not equal, but are designated as less than ($<$), greater than ($>$), less than or equal to ($\leq$) or greater than or equal to ($\geq$), it is called a linear inequality.  A linear inequality looks exactly like a linear equation, with the inequality sign replacing the equality sign.

For inequalities that contain variable expressions, you may be asked to solve the inequality for that variable. This just means that you need to find the values of the variable that make the inequality true.  

A linear inequality looks like a linear equation, with the inequality sign replacing the equal sign.  The same properties for solving an equation are used to solve an inequality; however, when solving an equation there is one solution (or one value that makes the equation true), but when solving an inequality there are many solutions (or values that make the statement true).

Solutions of Linear Inequalities

Example: Graph the solutions of the inequality: $x>4$

The solutions to this inequality includes every number that is greater than $4$ as shown below.

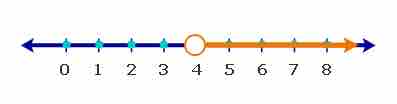
Inequality

Solutions to $x>4$ are graphed in yellow on the number line.  Notice the open circle means that the value of $4$ in not a solution to the inequality since $4>4$ is a false statement.  If the inequality was $x\geq 4$, then $4$ would be a solution and there would be a closed circle over the $4$ on the number line.

Solving Linear Inequalities

Solving the inequality is the same as solving an equation.  There is only one rule that is different: When you multiply or divide each side of an inequality by a negative number, you must reverse the inequality symbol to maintain a true statement.  

Example:  Solve the inequality: $-7x+3+x \leq 1-4x-10$

Step 1, combine like terms on each side of the inequality symbol:

$\displaystyle -6x+3\leq-4x-9$

Step 2, since there is a variable on both sides of the inequality, choose to move the $-4x$, to combine the variables on the left hand side of the inequality. 

Adding $4x$ yields: 

$\displaystyle -2x+3\leq-9$   

Step 3, this is similar to solving a two step equation. Subtract $3$:

 $\displaystyle -2x\leq-12$

Finally, divide both sides by $-2$ (remember to reverse the inequality symbol):

$\displaystyle x\ge 6$  

To read this answer, read from right to left, $x\geq6$. This reads "$x$ is greater than or equal to 6".