Multiplication of Two Monomials

A monomial is a single term consisting of a product of numbers and variables. It is a relative of the polynomial, which is an algebraic expression with more than one term. The following are examples of monomials:

• $3x$
• $6xy$
• $12$
• $4x^2$

(Note that multiplying monomials is not the same as adding algebraic expressions—monomials do not have to involve "like terms" in order to be combined together through multiplication.)

When you multiply monomials, you multiply their integer coefficients together and, if they contain any of the same variables, add the exponents on those variables together. 

For example:

• $(3x^2)(4x) = 12x^3$
• $(4xy)(5y^2) = 20xy^3$
• $(9)(2y^2) = 18y^2$
• $(5x)(3y) = 15xy$

Multiplication of Monomials and Polynomials

A monomial can be multiplied by a polynomial of any size (note that a polynomial is called a binomial if it has two terms and a trinomial if it has three terms). The monomial should be multiplied by each term in the polynomial separately. Any negative sign on a term should be included in the multiplication of that term. The resulting polynomial will have the same number of terms as the polynomial in the problem.

For example:

• $(2x)(x^2 + 5) = 2x^3 + 10x$
• $7(x^2y + 5) = 7x^2y + 35$
• $(x^3)(y^2 - 2x + 4) = x^3y^2 - 2x^4 + 4x^3$
• $-3x(2xy - 3y^2 - 2) = -6x^2y + 9xy^2 + 6x$

Multiplication of Two Binomials

Multiplying two binomials is less straightforward; however, there is a method that makes the process fairly convenient. "FOIL" is a mnemonic for the standard method of multiplying two binomials (hence the method is often referred to as the FOIL method). The word FOIL is an acronym for the four terms of the product:

• First (the "first" terms of each binomial are multiplied together)
• Outer (the "outside" terms are multiplied—i.e., the first term of the first binomial with the second term of the second)
• Inner (the "inside" terms are multiplied—i.e., the second term of the first binomial with the first term of the second)
• Last (the "last" terms of each binomial are multiplied together)

Once this process is complete, all the resulting terms are added together into a single polynomial.

Here is a visual depiction:

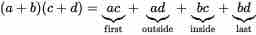
General form of the FOIL method

Demonstration of the FOIL method using variables.

The following diagram demonstrates this method slightly differently:

Diagram of the FOIL method

A visual demonstration of each step in the FOIL process.

Remember that any negative sign on a term in a binomial should also be included in the multiplication of that term. Additionally, remember to simplify the resulting polynomial if possible by combining like terms.

Example of Multiplying Binomials

Multiply the following binomials: 

$(2x + 1)(3x - 2)$

Following the FOIL method, multiply the first, outside, inside, and last terms:

$F: (2x)(3x) = 6x^2 \\ O: (2x)(-2) = -4x \\ I: (1)(3x) = 3x \\ L: (2)(-2) = -2 $

Now add all of these terms together:

$6x^2 - 4x + 3x - 2$

Notice that two of these terms are like terms ($-4x$ and $3x$) and can therefore be added together to simplify the expression further: 

$6x^2 - x - 2$