Solving a Rational Equation (Same Denominators)
For an equation that involves two fractions or rational expressions, cross-multiplying is a helpful strategy for simplifying the equation or determining the value of a variable.
For example, start with the following equation:
Cross-multiplying yields:
Now solve for
We could also use simple algebra. Start with the same equation:
Isolate the variable on the left by multiplying both sides by
The denominators on both sides cancel out, yielding:
You could also come to this conclusion through deductive reasoning. Notice that the rational expressions on both sides of the equal sign have the same denominator. If you have a rational equation where the denominators on either side of the equation are the same, then their respective numerators must also be the same value, even though they might be expressed in different terms. This suggests a strategy: Find a common denominator, set the numerators equal to each other, and solve for any unknowns.
Solving a Rational Equation (Different Denominators)
Several real-life situations can be modeled using equations that set two fractions, or ratios, to be equal to each other—for example, finding unknown dimensions of certain shapes.
Two triangles are said to be "similar" if they have equal corresponding angles. This is the same as the triangles having equal side-length ratios.
Similar geometric shapes
Two geometrical objects are similar if they both have the same shape or if one has the same shape as the mirror image of the other. In this image, figures shown in the same color are similar.
The two triangles below are similar. If length
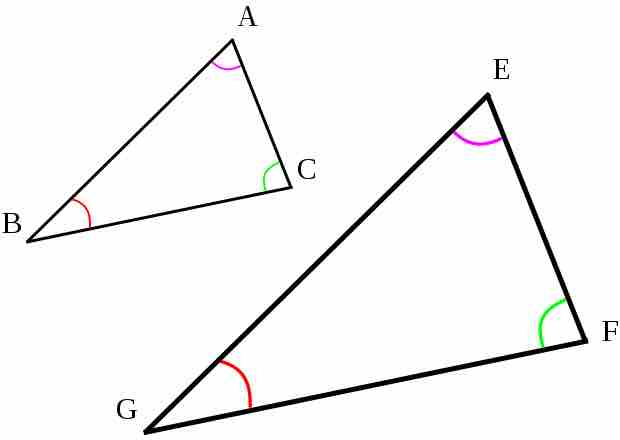
Similar triangles
Corresponding angles in similar shapes are marked with the same symbol. For example,
Let's start by writing a rational equation:
Now let's plug in the actual numbers:
Now cross-multiply:
Finally, divide both sides of the equation by 10:
Therefore,