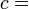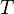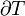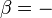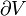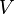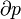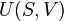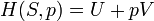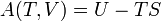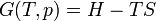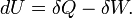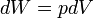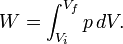Work (thermodynamics)
Background Information
SOS Children produced this website for schools as well as this video website about Africa. Do you want to know about sponsoring? See www.sponsorachild.org.uk
| Thermodynamics | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 The classical Carnot heat engine
|
|||||||||||||||||||||
|
Branches
|
|||||||||||||||||||||
|
Systems
State:
Equation of state Ideal gas · Real gas Phase of matter · Equilibrium Control volume · Instruments Processes: Isobaric · Isochoric · Isothermal Adiabatic · Isentropic · Isenthalpic Quasistatic · Polytropic Free expansion Reversibility · Irreversibility Endoreversibility Cycles: Heat engines · Heat pumps Thermal efficiency |
|||||||||||||||||||||
|
System properties
Property diagrams
Intensive and extensive properties Functions of state: Temperature / Entropy (intro.) † Pressure / Volume † Chemical potential / Particle no. † († Conjugate variables) Vapor quality Reduced properties Process functions: Work · Heat |
|||||||||||||||||||||
|
Material properties
|
|||||||||||||||||||||
|
Equations
Carnot's theorem · Clausius theorem · Fundamental relation · Ideal gas law · Maxwell relations · Onsager reciprocal relations · Bridgman's thermodynamic equations
Table of thermodynamic equations |
|||||||||||||||||||||
|
Potentials
|
|||||||||||||||||||||
|
History and culture
Philosophy:
Entropy and time · Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics History: General · Heat · Entropy · Gas laws Perpetual motion Theories: Caloric theory · Vis viva Theory of heat Mechanical equivalent of heat Motive power Publications: " An Experimental Enquiry Concerning ... Heat" " On the Equilibrium of Heterogeneous Substances" "Reflections on the Motive Power of Fire" Timelines of: Thermodynamics · Heat engines Art: Maxwell's thermodynamic surface Education: Entropy as energy dispersal |
|||||||||||||||||||||
In thermodynamics, work performed by a system is the energy transferred by the system to another that is accounted for by changes in the external generalized mechanical constraints on the system. As such, thermodynamic work is a generalization of the concept of mechanical work in mechanics.
The external generalized mechanical constraints may be chemical, electromagnetic (including radiative, as in laser power), gravitational, or pressure/volume or other simply mechanical constraints, including momental, as in radiative transfer. Thermodynamic work is defined to be measurable solely from knowledge of such external macroscopic constraint variables. These macroscopic variables always occur in conjugate pairs, for example pressure and volume, magnetic flux density and magnetization, mole fraction and chemical potential. In the SI system of measurement, work is measured in joules (symbol: J). The rate at which work is performed is power.
History
1824
Work, i.e. "weight lifted through a height", was originally defined in 1824 by Sadi Carnot in his famous paper Reflections on the Motive Power of Fire. Specifically, according to Carnot:
- We use here motive power (work) to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised.
1845
In 1845, the English physicist James Joule wrote a paper On the mechanical equivalent of heat for the British Association meeting in Cambridge. In this work, he reported his best-known experiment, in which the work released through the action of a "weight falling through a height" was used to turn a paddle-wheel in an insulated barrel of water.
In this experiment, the friction and agitation of the paddle-wheel on the body of water caused heat to be generated which, in turn, increased the temperature of water. Both the temperature change ∆T of the water and the height of the fall ∆h of the weight mg were recorded. Using these values, Joule was able to determine the mechanical equivalent of heat. Joule estimated a mechanical equivalent of heat to be 819 ft•lbf/Btu (4.41 J/cal). The modern day definitions of heat, work, temperature, and energy all have connection to this experiment.
Overview
The first law of thermodynamics relates changes in the internal energy of a thermodynamic system to two forms of energy transfer.
The concept of thermodynamic work is more general than that of simple mechanical work because it includes other types of energy transfers as well. An extremely important fact to understand is that thermodynamic work is strictly and fully defined by its external generalized mechanical variables. The other form of energy transfer is heat. Heat is measured by change of temperature of a known quantity of calorimetric material substance; it is of the essence of heat that it is not defined by the external generalized mechanical variables that define work. This distinction between work and heat is the crucial essence of thermodynamics.
Work refers to forms of energy transfer which can be accounted for in terms of changes in the external macroscopic physical constraints on the system, for example energy which goes into expanding the volume of a system against an external pressure, by driving a piston-head out of a cylinder against an external force. The electrical work required to move a charge against an external electrical field can be measured.
This is in contrast to heat, which is the energy that is carried into or out of the system in the form of transfers in the microscopic thermal motions of particles, or by thermal radiation. There are just five forms of heat transfer: conduction, radiation, diffusion, friction, bulk and shear viscosity, and phase change. Convection of energy is not, as sometimes mistakenly supposed (a relic of the caloric theory of heat), a form of transfer of heat, because convection is not in itself a microscopic motion of microscopic particles or photons, but is a bulk flow of ponderable matter with its internal energy. Because, according to the zeroth law of thermodynamics, there is only one kind of heat, it is possible to define also a macroscopic variable conjugate to temperature, namely entropy.
Formal definition
According to the first law of thermodynamics, any net increase in the internal energy U of a thermodynamic system must be fully accounted for, in terms of heat δQ entering the system and the work δW done by the system:
The letter d indicates an exact differential, expressing that internal energy U is a property of the state of the system; they depend only on the original state and the final state, and not upon the path taken. In contrast, the Greek delta's (δ‘s) in this equation reflect the fact that the heat transfer and the work transfer are not properties of the final state of the system. Given only the initial state and the final state of the system, one can only say what the total change in internal energy was, not how much of the energy went out as heat, and how much as work. This can be summarized by saying that heat and work are not state functions of the system.
Pressure-volume work
Pressure-volume work, (or pV work) occurs when the volume (V) of a system changes. pV work is often measured in units of litre-atmospheres (not SI), where 1L·atm = 101.325J. pV work is an important topic in chemical thermodynamics.
pV work is represented by the following differential equation:
where:
- W = work done on the system
- p = pressure
- V = volume
The above equation of work is valid for any reversible process of a closed system.
The first law of thermodynamics can therefore be expressed as
Path dependence
Like all work functions, in general PV work is path-dependent and is therefore a thermodynamic process function. However in the specific case of a reversible adiabatic process, work does not depend on the path. The first law of thermodynamics states 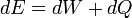 . For an adiabatic process,
. For an adiabatic process, 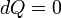 and thus the work done must be equivalent to a change in internal energy only, which is proportional to the net change in temperature. Since the work depends only on the temperature change, it is therefore not dependent on the specific path taken.
and thus the work done must be equivalent to a change in internal energy only, which is proportional to the net change in temperature. Since the work depends only on the temperature change, it is therefore not dependent on the specific path taken.
If the process took a path other than the adiabatic path, the work would be different. This would only be possible if heat flowed into / out of the system, i.e., it would not be adiabatic. In a given system, there are numerous paths between two temperatures, and there are numerous paths which are adiabatic. But there is only one adiabatic path between two temperatures. Starting at some initial temperature, each adiabatic path would lead to a different final temperature. But between two given temperatures, there is only one way for 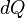 to be zero, but there are many ways for it to be nonzero.
to be zero, but there are many ways for it to be nonzero.
In mathematical terms, the differential  is an inexact differential; however in the path independent case it can be shown to be an exact differential. Again from the first law,
is an inexact differential; however in the path independent case it can be shown to be an exact differential. Again from the first law,  . Note that
. Note that 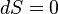 for a reversible process, thus
for a reversible process, thus  , which is exact. Because the work differential is exact, work can be computed in a path-independent manner.
, which is exact. Because the work differential is exact, work can be computed in a path-independent manner.
To be more rigorous, it should be written đW (with a line through the d). In other words, đW is not an exact one-form. The line-through is merely a flag to warn us there is actually no function ( 0-form)  which is the potential of đW. If there were, indeed, this function
which is the potential of đW. If there were, indeed, this function  , we should be able to just use Stokes Theorem to evaluate this putative function, the potential of đW, at the boundary of the path, that is, the initial and final points, and therefore the work would be a state function. This impossibility is consistent with the fact that it does not make sense to refer to the work on a point in the pV diagram; work presupposes a path.
, we should be able to just use Stokes Theorem to evaluate this putative function, the potential of đW, at the boundary of the path, that is, the initial and final points, and therefore the work would be a state function. This impossibility is consistent with the fact that it does not make sense to refer to the work on a point in the pV diagram; work presupposes a path.
Free energy and exergy
The amount of useful work which may be extracted from a thermodynamic system is determined by the second law of thermodynamics. Under many practical situations this can be represented by the thermodynamic availability, or Exergy, function. Two important cases are: in thermodynamic systems where the temperature and volume are held constant, the measure of useful work attainable is the Helmholtz free energy function; and in systems where the temperature and pressure are held constant, the measure of useful work attainable is the Gibbs free energy.